Rapid Likelihood Free Inference of Compact Binary Coalescences using Accelerated Hardware

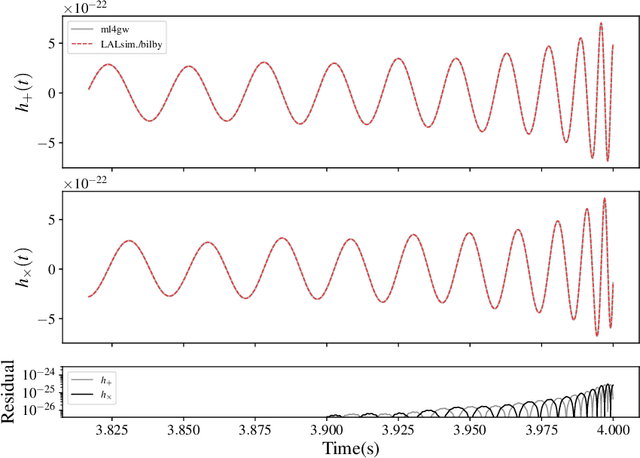
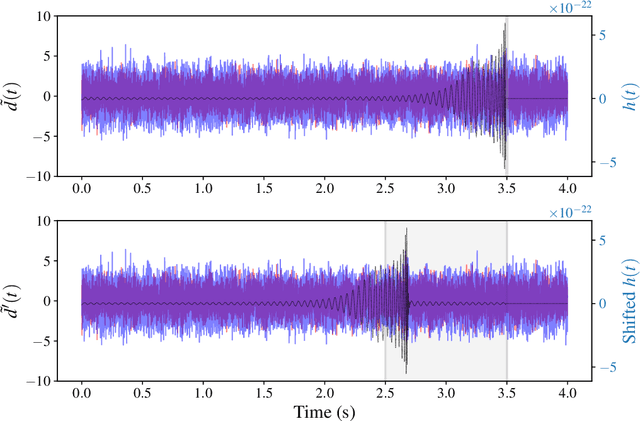
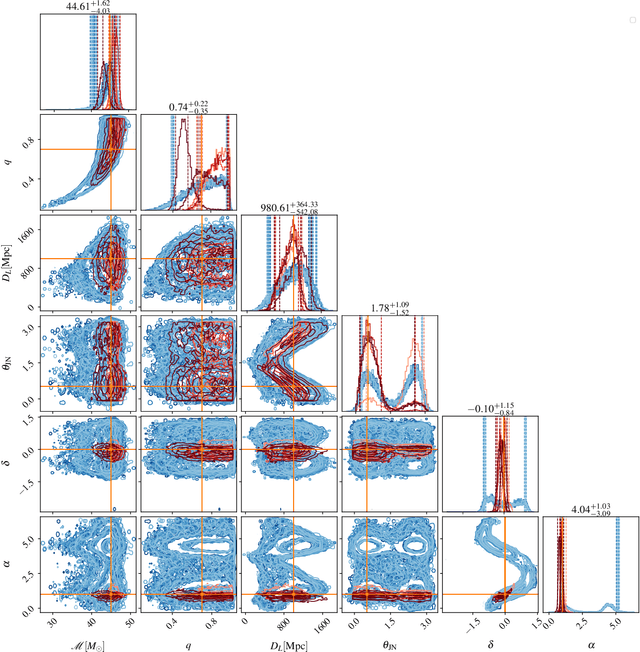
We report a gravitational-wave parameter estimation algorithm, AMPLFI, based on likelihood-free inference using normalizing flows. The focus of AMPLFI is to perform real-time parameter estimation for candidates detected by machine-learning based compact binary coalescence search, Aframe. We present details of our algorithm and optimizations done related to data-loading and pre-processing on accelerated hardware. We train our model using binary black-hole (BBH) simulations on real LIGO-Virgo detector noise. Our model has $\sim 6$ million trainable parameters with training times $\lesssim 24$ hours. Based on online deployment on a mock data stream of LIGO-Virgo data, Aframe + AMPLFI is able to pick up BBH candidates and infer parameters for real-time alerts from data acquisition with a net latency of $\sim 6$s.

Optimizing Likelihood-free Inference using Self-supervised Neural Symmetry Embeddings

Likelihood-free inference is quickly emerging as a powerful tool to perform fast/effective parameter estimation. We demonstrate a technique of optimizing likelihood-free inference to make it even faster by marginalizing symmetries in a physical problem. In this approach, physical symmetries, for example, time-translation are learned using joint-embedding via self-supervised learning with symmetry data augmentations. Subsequently, parameter inference is performed using a normalizing flow where the embedding network is used to summarize the data before conditioning the parameters. We present this approach on two simple physical problems and we show faster convergence in a smaller number of parameters compared to a normalizing flow that does not use a pre-trained symmetry-informed representation.