Exploring Neural Network Pruning with Screening Methods

Deep neural networks (DNNs) such as convolutional neural networks (CNNs) for visual tasks, recurrent neural networks (RNNs) for sequence data, and transformer models for rich linguistic or multimodal tasks, achieved unprecedented performance on a wide range of tasks. The impressive performance of modern DNNs is partially attributed to their sheer scale. The latest deep learning models have tens to hundreds of millions of parameters which makes the inference processes resource-intensive. The high computational complexity of these networks prevents their deployment on resource-limited devices such as mobile platforms, IoT devices, and edge computing systems because these devices require energy-efficient and real-time processing capabilities. This paper proposes and evaluates a network pruning framework that eliminates non-essential parameters based on a statistical analysis of network component significance across classification categories. The proposed method uses screening methods coupled with a weighted scheme to assess connection and channel contributions for unstructured and structured pruning which allows for the elimination of unnecessary network elements without significantly degrading model performance. Extensive experimental validation on real-world vision datasets for both fully connected neural networks (FNNs) and CNNs has shown that the proposed framework produces competitive lean networks compared to the original networks. Moreover, the proposed framework outperforms state-of-art network pruning methods in two out of three cases.

Neural Rule Ensembles: Encoding Sparse Feature Interactions into Neural Networks

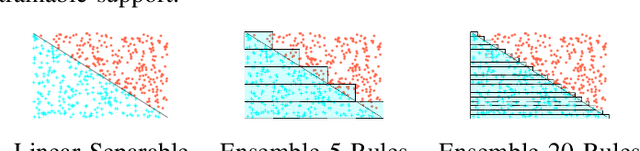
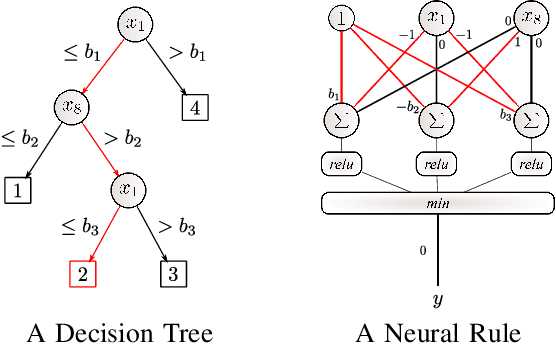
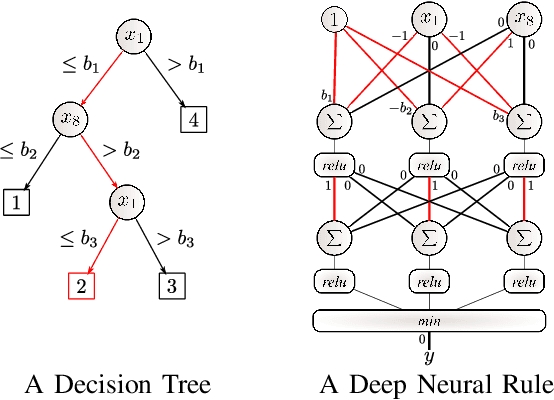
Artificial Neural Networks form the basis of very powerful learning methods. It has been observed that a naive application of fully connected neural networks to data with many irrelevant variables often leads to overfitting. In an attempt to circumvent this issue, a prior knowledge pertaining to what features are relevant and their possible feature interactions can be encoded into these networks. In this work, we use decision trees to capture such relevant features and their interactions and define a mapping to encode extracted relationships into a neural network. This addresses the initialization related concern of fully connected neural networks. At the same time through feature selection it enables learning of compact representations compared to state of the art tree-based approaches. Empirical evaluations and simulation studies show the superiority of such an approach over fully connected neural networks and tree-based approaches

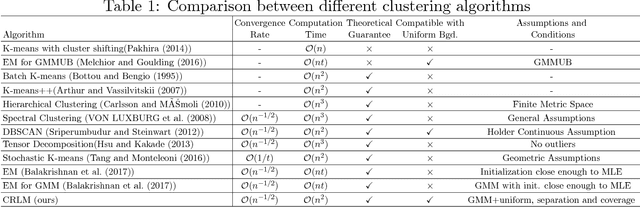
Unsupervised Learning of Mixture Models with a Uniform Background Component

Gaussian Mixture Models are one of the most studied and mature models in unsupervised learning. However, outliers are often present in the data and could influence the cluster estimation. In this paper, we study a new model that assumes that data comes from a mixture of a number of Gaussians as well as a uniform "background" component assumed to contain outliers and other non-interesting observations. We develop a novel method based on robust loss minimization that performs well in clustering such GMM with a uniform background. We give theoretical guarantees for our clustering algorithm to obtain best clustering results with high probability. Besides, we show that the result of our algorithm does not depend on initialization or local optima, and the parameter tuning is an easy task. By numeric simulations, we demonstrate that our algorithm enjoys high accuracy and achieves the best clustering results given a large enough sample size. Finally, experimental comparisons with typical clustering methods on real datasets witness the potential of our algorithm in real applications.