Unsupervised Learning of Mixture Models with a Uniform Background Component

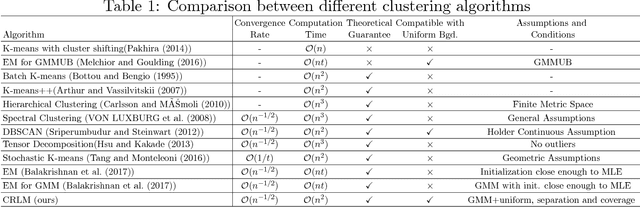
Gaussian Mixture Models are one of the most studied and mature models in unsupervised learning. However, outliers are often present in the data and could influence the cluster estimation. In this paper, we study a new model that assumes that data comes from a mixture of a number of Gaussians as well as a uniform "background" component assumed to contain outliers and other non-interesting observations. We develop a novel method based on robust loss minimization that performs well in clustering such GMM with a uniform background. We give theoretical guarantees for our clustering algorithm to obtain best clustering results with high probability. Besides, we show that the result of our algorithm does not depend on initialization or local optima, and the parameter tuning is an easy task. By numeric simulations, we demonstrate that our algorithm enjoys high accuracy and achieves the best clustering results given a large enough sample size. Finally, experimental comparisons with typical clustering methods on real datasets witness the potential of our algorithm in real applications.