Neural Rule Ensembles: Encoding Sparse Feature Interactions into Neural Networks

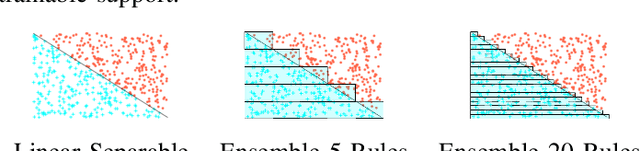
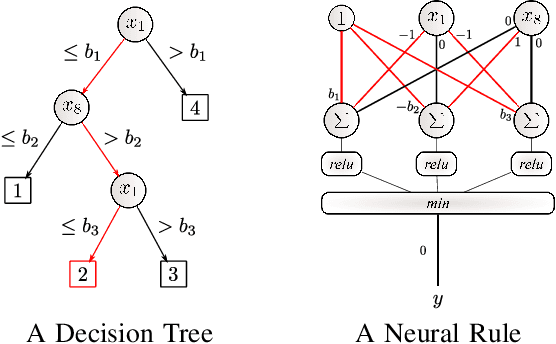
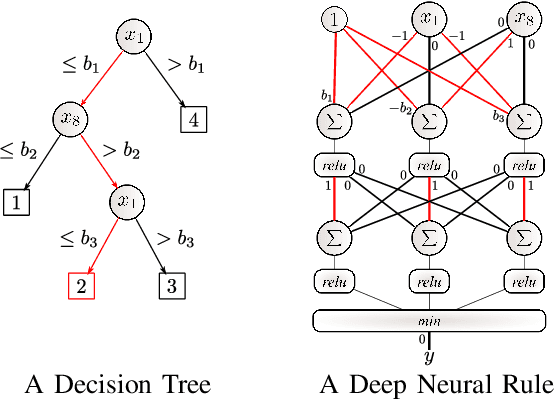
Artificial Neural Networks form the basis of very powerful learning methods. It has been observed that a naive application of fully connected neural networks to data with many irrelevant variables often leads to overfitting. In an attempt to circumvent this issue, a prior knowledge pertaining to what features are relevant and their possible feature interactions can be encoded into these networks. In this work, we use decision trees to capture such relevant features and their interactions and define a mapping to encode extracted relationships into a neural network. This addresses the initialization related concern of fully connected neural networks. At the same time through feature selection it enables learning of compact representations compared to state of the art tree-based approaches. Empirical evaluations and simulation studies show the superiority of such an approach over fully connected neural networks and tree-based approaches

Random Hinge Forest for Differentiable Learning

We propose random hinge forests, a simple, efficient, and novel variant of decision forests. Importantly, random hinge forests can be readily incorporated as a general component within arbitrary computation graphs that are optimized end-to-end with stochastic gradient descent or variants thereof. We derive random hinge forest and ferns, focusing on their sparse and efficient nature, their min-max margin property, strategies to initialize them for arbitrary network architectures, and the class of optimizers most suitable for optimizing random hinge forest. The performance and versatility of random hinge forests are demonstrated by experiments incorporating a variety of of small and large UCI machine learning data sets and also ones involving the MNIST, Letter, and USPS image datasets. We compare random hinge forests with random forests and the more recent backpropagating deep neural decision forests.

Relevant Ensemble of Trees

Tree ensembles are flexible predictive models that can capture relevant variables and to some extent their interactions in a compact and interpretable manner. Most algorithms for obtaining tree ensembles are based on versions of boosting or Random Forest. Previous work showed that boosting algorithms exhibit a cyclic behavior of selecting the same tree again and again due to the way the loss is optimized. At the same time, Random Forest is not based on loss optimization and obtains a more complex and less interpretable model. In this paper we present a novel method for obtaining compact tree ensembles by growing a large pool of trees in parallel with many independent boosting threads and then selecting a small subset and updating their leaf weights by loss optimization. We allow for the trees in the initial pool to have different depths which further helps with generalization. Experiments on real datasets show that the obtained model has usually a smaller loss than boosting, which is also reflected in a lower misclassification error on the test set.