Constant Rate Schedule: Constant-Rate Distributional Change for Efficient Training and Sampling in Diffusion Models

We propose a noise schedule that ensures a constant rate of change in the probability distribution of diffused data throughout the diffusion process. To obtain this noise schedule, we measure the rate of change in the probability distribution of the forward process and use it to determine the noise schedule before training diffusion models. The functional form of the noise schedule is automatically determined and tailored to each dataset and type of diffusion model. We evaluate the effectiveness of our noise schedule on unconditional and class-conditional image generation tasks using the LSUN (bedroom/church/cat/horse), ImageNet, and FFHQ datasets. Through extensive experiments, we confirmed that our noise schedule broadly improves the performance of the diffusion models regardless of the dataset, sampler, number of function evaluations, or type of diffusion model.

Optimization of neural networks via finite-value quantum fluctuations

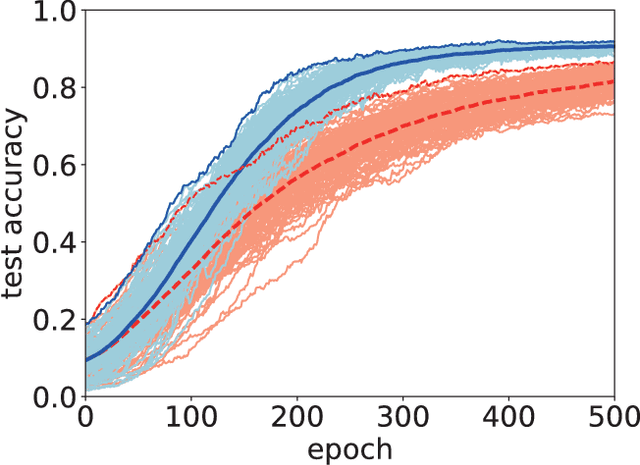
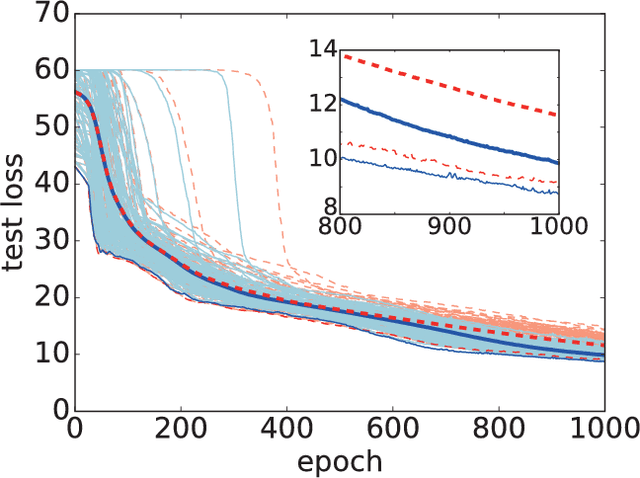
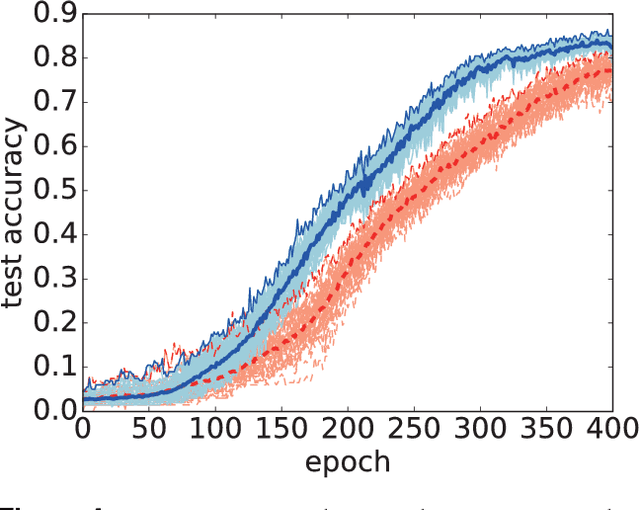
We numerically test an optimization method for deep neural networks (DNNs) using quantum fluctuations inspired by quantum annealing. For efficient optimization, our method utilizes the quantum tunneling effect beyond the potential barriers. The path integral formulation of the DNN optimization generates an attracting force to simulate the quantum tunneling effect. In the standard quantum annealing method, the quantum fluctuations will vanish at the last stage of optimization. In this study, we propose a learning protocol that utilizes a finite value for quantum fluctuations strength to obtain higher generalization performance, which is a type of robustness. We demonstrate the performance of our method using two well-known open datasets: the MNIST dataset and the Olivetti face dataset. Although computational costs prevent us from testing our method on large datasets with high-dimensional data, results show that our method can enhance generalization performance by induction of the finite value for quantum fluctuations.