LeMoLE: LLM-Enhanced Mixture of Linear Experts for Time Series Forecasting

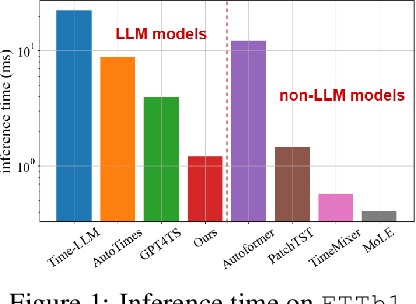
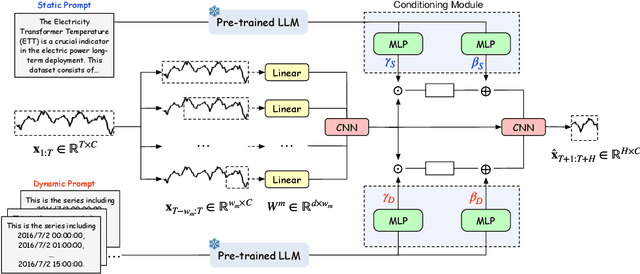
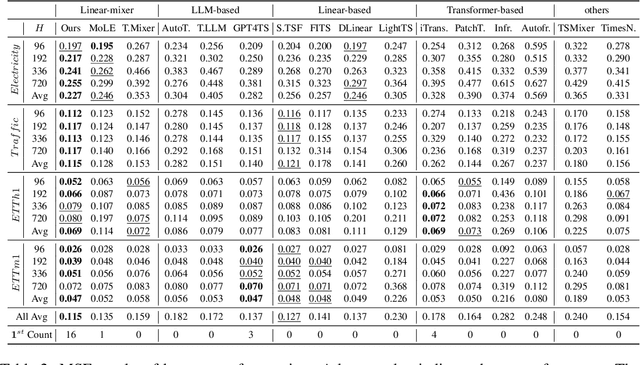
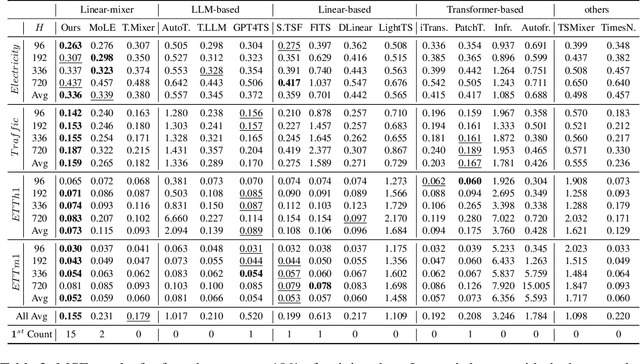
Recent research has shown that large language models (LLMs) can be effectively used for real-world time series forecasting due to their strong natural language understanding capabilities. However, aligning time series into semantic spaces of LLMs comes with high computational costs and inference complexity, particularly for long-range time series generation. Building on recent advancements in using linear models for time series, this paper introduces an LLM-enhanced mixture of linear experts for precise and efficient time series forecasting. This approach involves developing a mixture of linear experts with multiple lookback lengths and a new multimodal fusion mechanism. The use of a mixture of linear experts is efficient due to its simplicity, while the multimodal fusion mechanism adaptively combines multiple linear experts based on the learned features of the text modality from pre-trained large language models. In experiments, we rethink the need to align time series to LLMs by existing time-series large language models and further discuss their efficiency and effectiveness in time series forecasting. Our experimental results show that the proposed LeMoLE model presents lower prediction errors and higher computational efficiency than existing LLM models.

MCCoder: Streamlining Motion Control with LLM-Assisted Code Generation and Rigorous Verification

Large Language Models (LLMs) have shown considerable promise in code generation. However, the automation sector, especially in motion control, continues to rely heavily on manual programming due to the complexity of tasks and critical safety considerations. In this domain, incorrect code execution can pose risks to both machinery and personnel, necessitating specialized expertise. To address these challenges, we introduce MCCoder, an LLM-powered system designed to generate code that addresses complex motion control tasks, with integrated soft-motion data verification. MCCoder enhances code generation through multitask decomposition, hybrid retrieval-augmented generation (RAG), and self-correction with a private motion library. Moreover, it supports data verification by logging detailed trajectory data and providing simulations and plots, allowing users to assess the accuracy of the generated code and bolstering confidence in LLM-based programming. To ensure robust validation, we propose MCEVAL, an evaluation dataset with metrics tailored to motion control tasks of varying difficulties. Experiments indicate that MCCoder improves performance by 11.61% overall and by 66.12% on complex tasks in MCEVAL dataset compared with base models with naive RAG. This system and dataset aim to facilitate the application of code generation in automation settings with strict safety requirements. MCCoder is publicly available at https://github.com/MCCodeAI/MCCoder.

A Domain-adaptive Physics-informed Neural Network for Inverse Problems of Maxwell's Equations in Heterogeneous Media

Maxwell's equations are a collection of coupled partial differential equations (PDEs) that, together with the Lorentz force law, constitute the basis of classical electromagnetism and electric circuits. Effectively solving Maxwell's equations is crucial in various fields, like electromagnetic scattering and antenna design optimization. Physics-informed neural networks (PINNs) have shown powerful ability in solving PDEs. However, PINNs still struggle to solve Maxwell's equations in heterogeneous media. To this end, we propose a domain-adaptive PINN (da-PINN) to solve inverse problems of Maxwell's equations in heterogeneous media. First, we propose a location parameter of media interface to decompose the whole domain into several sub-domains. Furthermore, the electromagnetic interface conditions are incorporated into a loss function to improve the prediction performance near the interface. Then, we propose a domain-adaptive training strategy for da-PINN. Finally, the effectiveness of da-PINN is verified with two case studies.