Heavy-Ball Momentum Accelerated Actor-Critic With Function Approximation

By using an parametric value function to replace the Monte-Carlo rollouts for value estimation, the actor-critic (AC) algorithms can reduce the variance of stochastic policy gradient so that to improve the convergence rate. While existing works mainly focus on analyzing convergence rate of AC algorithms under Markovian noise, the impacts of momentum on AC algorithms remain largely unexplored. In this work, we first propose a heavy-ball momentum based advantage actor-critic (\mbox{HB-A2C}) algorithm by integrating the heavy-ball momentum into the critic recursion that is parameterized by a linear function. When the sample trajectory follows a Markov decision process, we quantitatively certify the acceleration capability of the proposed HB-A2C algorithm. Our theoretical results demonstrate that the proposed HB-A2C finds an $\epsilon$-approximate stationary point with $\oo{\epsilon^{-2}}$ iterations for reinforcement learning tasks with Markovian noise. Moreover, we also reveal the dependence of learning rates on the length of the sample trajectory. By carefully selecting the momentum factor of the critic recursion, the proposed HB-A2C can balance the errors introduced by the initialization and the stoschastic approximation.

Variance-Reduced Proximal and Splitting Schemes for Monotone Stochastic Generalized Equations

We consider monotone inclusion problems where the operators may be expectation-valued. A direct application of proximal and splitting schemes is complicated by resolving problems with expectation-valued maps at each step, a concern that is addressed by using sampling. Accordingly, we propose avenues for addressing uncertainty in the mapping. (i) Variance-reduced stochastic proximal point method (vr-SPP). We develop amongst the first variance-reduced stochastic proximal-point schemes that achieves deterministic rates of convergence in terms of solving proximal-point problems. In addition, it is shown that the schemes are characterized by either optimal or near-optimal oracle (or sample) complexity guarantees. Finally, the generated sequences are shown to be convergent to a solution in an almost-sure sense in both monotone and strongly monotone regimes; (ii) Variance-reduced stochastic modified forward-backward splitting scheme (vr-SMFBS). In constrained settings, we consider structured settings when the map can be decomposed into an expectation-valued map $A$ and a maximal monotone map $B$ with a tractable resolvent. Akin to (i), we show that the proposed schemes are equipped with a.s. convergence guarantees, linear (strongly monotone $A$) and $\mathcal{O}(1/k)$ (monotone $A$) rates of convergence while achieving optimal oracle complexity bounds. Of these, the rate statements in monotone regimes rely on leveraging the Fitzpatrick gap function for monotone inclusions. Furthermore, the schemes rely on weaker moment requirements on noise as well as allow for weakening unbiasedness requirements on oracles in strongly monotone regimes. Preliminary numerics reflect these findings and show that the variance-reduced schemes outperform stochastic approximation schemes, stochastic splitting and proximal point schemes, and sample-average approximation approaches.

Development of modeling and control strategies for an approximated Gaussian process

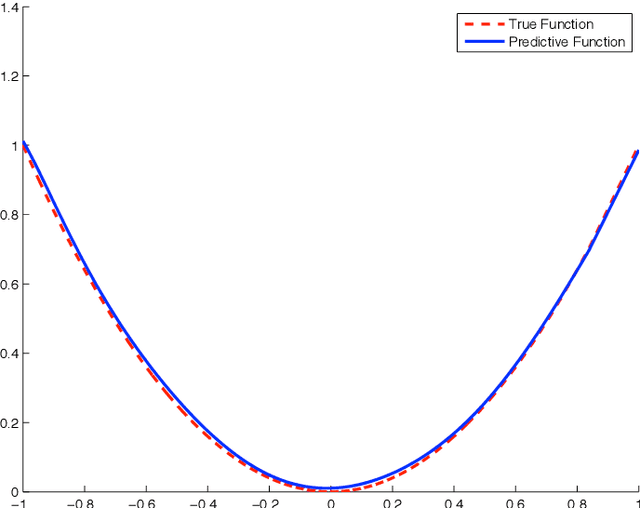
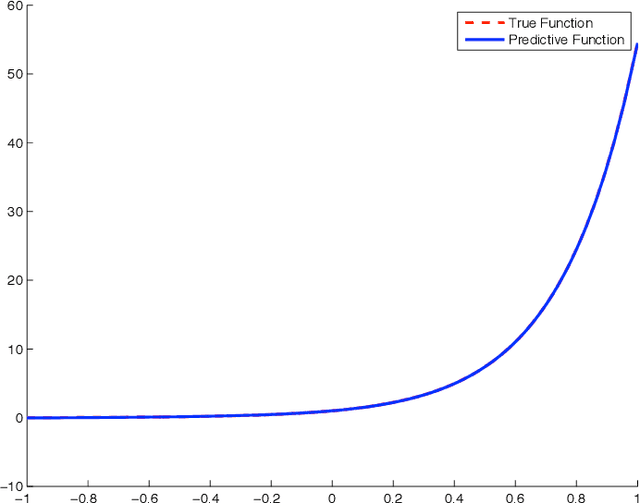
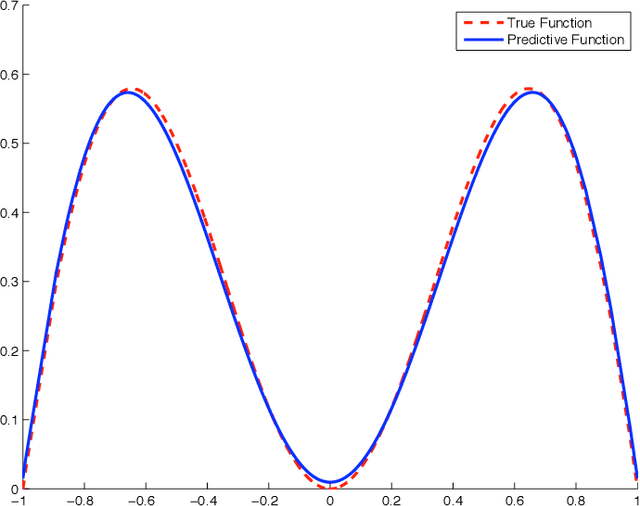
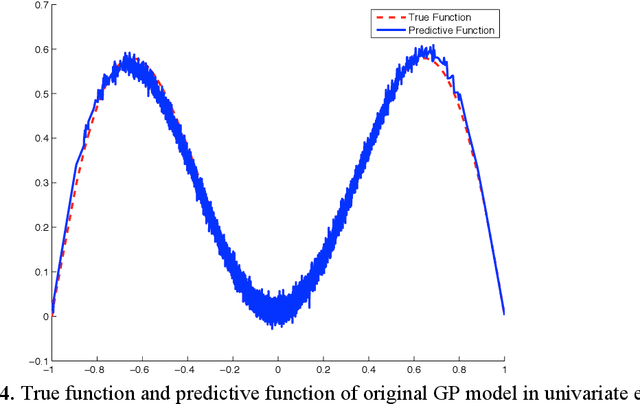
The Gaussian process (GP) model, which has been extensively applied as priors of functions, has demonstrated excellent performance. The specification of a large number of parameters affects the computational efficiency and the feasibility of implementation of a control strategy. We propose a linear model to approximate GPs; this model expands the GP model by a series of basis functions. Several examples and simulation studies are presented to demonstrate the advantages of the proposed method. A control strategy is provided with the proposed linear model.