Fibrational Initial Algebra-Final Coalgebra Coincidence over Initial Algebras: Turning Verification Witnesses Upside Down

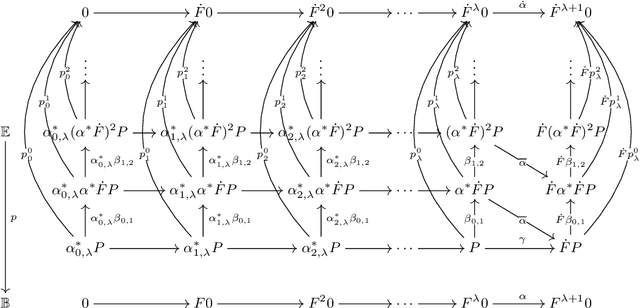
The coincidence between initial algebras (IAs) and final coalgebras (FCs) is a phenomenon that underpins various important results in theoretical computer science. In this paper, we identify a general fibrational condition for the IA-FC coincidence, namely in the fiber over an initial algebra in the base category. Identifying (co)algebras in a fiber as (co)inductive predicates, our fibrational IA-FC coincidence allows one to use coinductive witnesses (such as invariants) for verifying inductive properties (such as liveness). Our general fibrational theory features the technical condition of stability of chain colimits; we extend the framework to the presence of a monadic effect, too, restricting to fibrations of complete lattice-valued predicates. Practical benefits of our categorical theory are exemplified by new "upside-down" witness notions for three verification problems: probabilistic liveness, and acceptance and model-checking with respect to bottom-up tree automata.

Control-Data Separation and Logical Condition Propagation for Efficient Inference on Probabilistic Programs

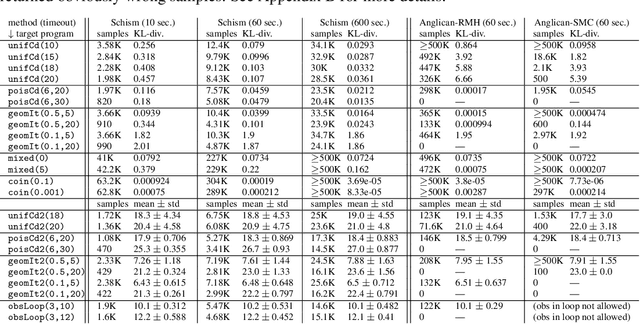
We introduce a novel sampling algorithm for Bayesian inference on imperative probabilistic programs. It features a hierarchical architecture that separates control flows from data: the top-level samples a control flow, and the bottom level samples data values along the control flow picked by the top level. This separation allows us to plug various language-based analysis techniques in probabilistic program sampling; specifically, we use logical backward propagation of observations for sampling efficiency. We implemented our algorithm on top of Anglican. The experimental results demonstrate our algorithm's efficiency, especially for programs with while loops and rare observations.

Differentiable Causal Computations via Delayed Trace

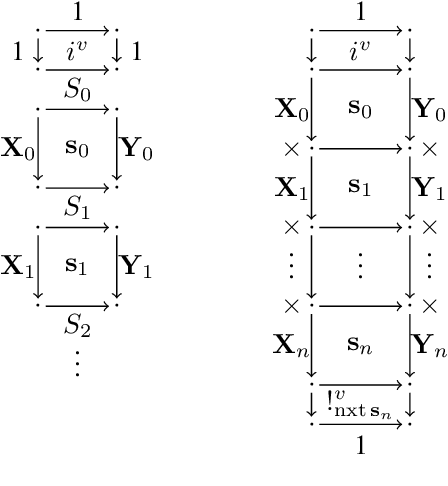
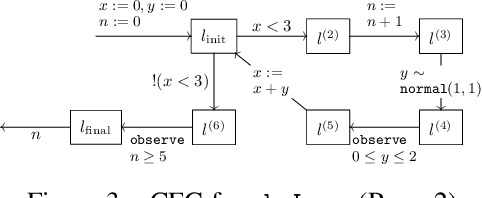
We investigate causal computations taking sequences of inputs to sequences of outputs where the $n$th output depends on the first $n$ inputs only. We model these in category theory via a construction taking a Cartesian category $C$ to another category $St(C)$ with a novel trace-like operation called "delayed trace", which misses yanking and dinaturality axioms of the usual trace. The delayed trace operation provides a feedback mechanism in $St(C)$ with an implicit guardedness guarantee. When $C$ is equipped with a Cartesian differential operator, we construct a differential operator for $St(C)$ using an abstract version of backpropagation through time, a technique from machine learning based on unrolling of functions. This obtains a swath of properties for backpropagation through time, including a chain rule and Schwartz theorem. Our differential operator is also able to compute the derivative of a stateful network without requiring the network to be unrolled.