Functorial String Diagrams for Reverse-Mode Automatic Differentiation

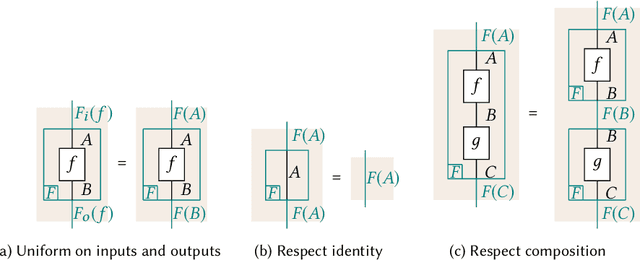
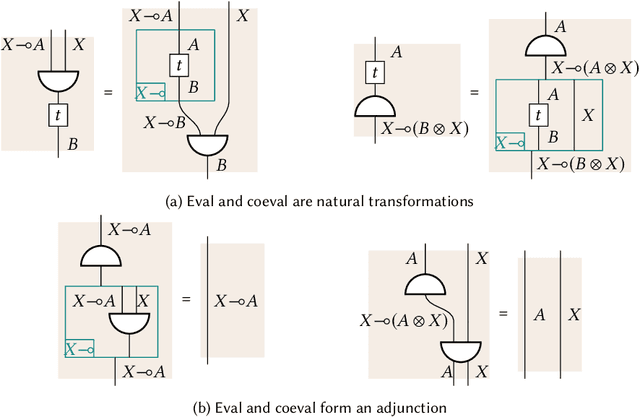
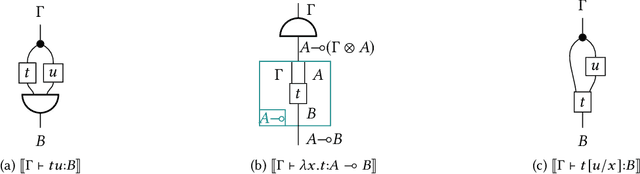
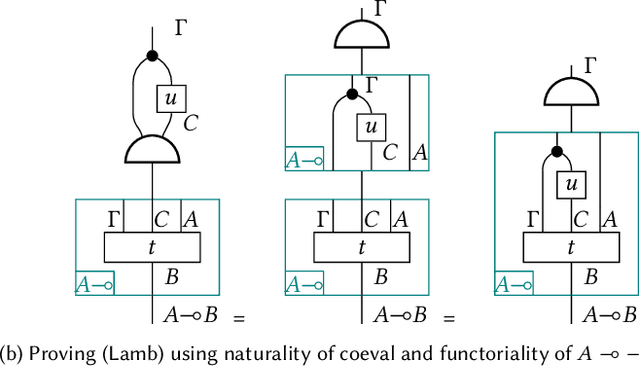
We enhance the calculus of string diagrams for monoidal categories with hierarchical features in order to capture closed monoidal (and cartesian closed) structure. Using this new syntax we formulate an automatic differentiation algorithm for (applied) simply typed lambda calculus in the style of [Pearlmutter and Siskind 2008] and we prove for the first time its soundness. To give an efficient yet principled implementation of the AD algorithm we define a sound and complete representation of hierarchical string diagrams as a class of hierarchical hypergraphs we call hypernets.

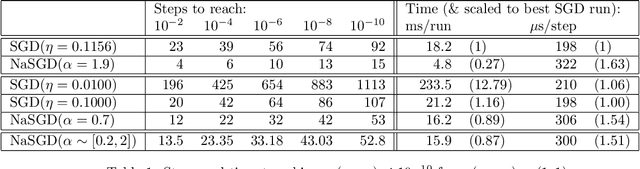
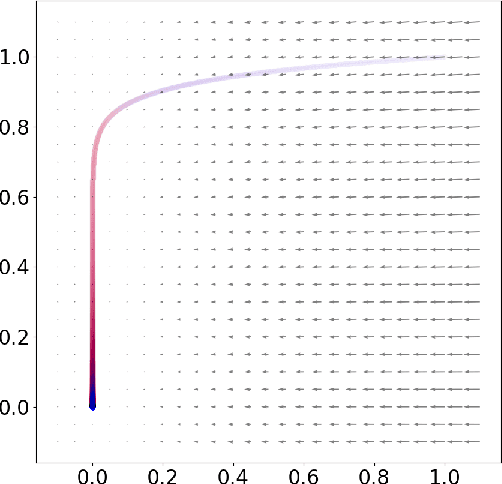
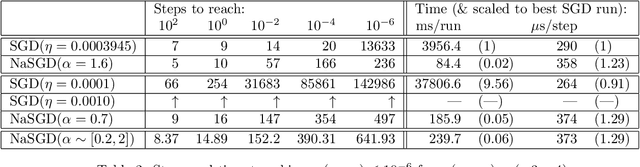
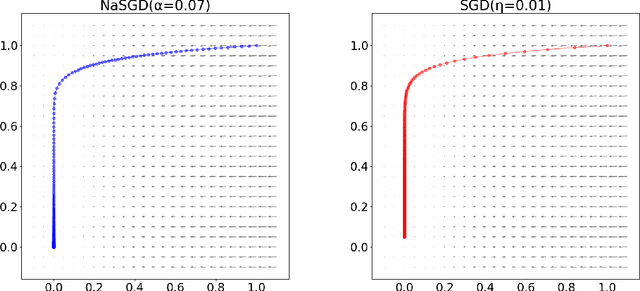
Reparametrizing gradient descent

In this work, we propose an optimization algorithm which we call norm-adapted gradient descent. This algorithm is similar to other gradient-based optimization algorithms like Adam or Adagrad in that it adapts the learning rate of stochastic gradient descent at each iteration. However, rather than using statistical properties of observed gradients, norm-adapted gradient descent relies on a first-order estimate of the effect of a standard gradient descent update step, much like the Newton-Raphson method in many dimensions. Our algorithm can also be compared to quasi-Newton methods, but we seek roots rather than stationary points. Seeking roots can be justified by the fact that for models with sufficient capacity measured by nonnegative loss functions, roots coincide with global optima. This work presents several experiments where we have used our algorithm; in these results, it appears norm-adapted descent is particularly strong in regression settings but is also capable of training classifiers.

Differentiable Causal Computations via Delayed Trace

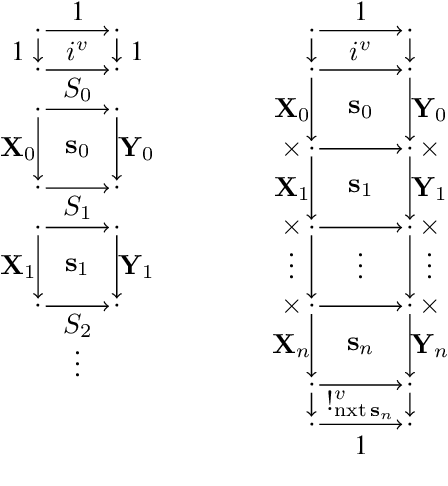
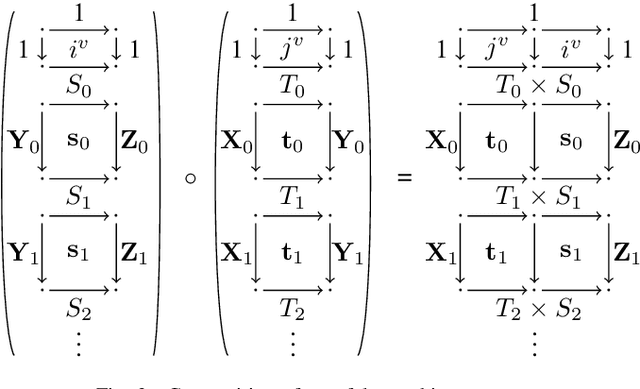
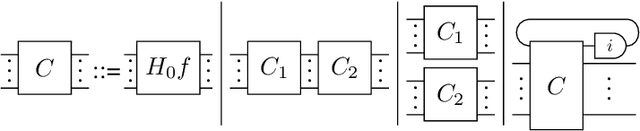
We investigate causal computations taking sequences of inputs to sequences of outputs where the $n$th output depends on the first $n$ inputs only. We model these in category theory via a construction taking a Cartesian category $C$ to another category $St(C)$ with a novel trace-like operation called "delayed trace", which misses yanking and dinaturality axioms of the usual trace. The delayed trace operation provides a feedback mechanism in $St(C)$ with an implicit guardedness guarantee. When $C$ is equipped with a Cartesian differential operator, we construct a differential operator for $St(C)$ using an abstract version of backpropagation through time, a technique from machine learning based on unrolling of functions. This obtains a swath of properties for backpropagation through time, including a chain rule and Schwartz theorem. Our differential operator is also able to compute the derivative of a stateful network without requiring the network to be unrolled.

Neural Nets via Forward State Transformation and Backward Loss Transformation

This article studies (multilayer perceptron) neural networks with an emphasis on the transformations involved --- both forward and backward --- in order to develop a semantical/logical perspective that is in line with standard program semantics. The common two-pass neural network training algorithms make this viewpoint particularly fitting. In the forward direction, neural networks act as state transformers. In the reverse direction, however, neural networks change losses of outputs to losses of inputs, thereby acting like a (real-valued) predicate transformer. In this way, backpropagation is functorial by construction, as shown earlier in recent other work. We illustrate this perspective by training a simple instance of a neural network.