Overdrawing Urns using Categories of Signed Probabilities

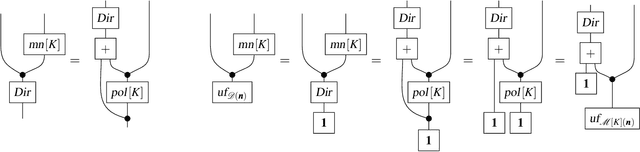
A basic experiment in probability theory is drawing without replacement from an urn filled with multiple balls of different colours. Clearly, it is physically impossible to overdraw, that is, to draw more balls from the urn than it contains. This paper demonstrates that overdrawing does make sense mathematically, once we allow signed distributions with negative probabilities. A new (conservative) extension of the familiar hypergeometric ('draw-and-delete') distribution is introduced that allows draws of arbitrary sizes, including overdraws. The underlying theory makes use of the dual basis functions of the Bernstein polynomials, which play a prominent role in computer graphics. Negative probabilities are treated systematically in the framework of categorical probability and the central role of datastructures such as multisets and monads is emphasised.

Pearl's and Jeffrey's Update as Modes of Learning in Probabilistic Programming

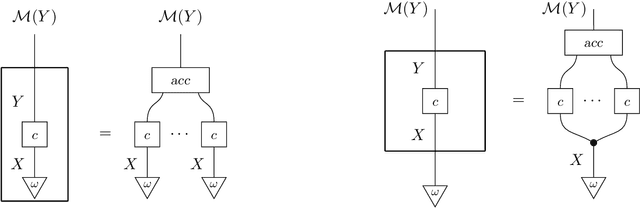
The concept of updating a probability distribution in the light of new evidence lies at the heart of statistics and machine learning. Pearl's and Jeffrey's rule are two natural update mechanisms which lead to different outcomes, yet the similarities and differences remain mysterious. This paper clarifies their relationship in several ways: via separate descriptions of the two update mechanisms in terms of probabilistic programs and sampling semantics, and via different notions of likelihood (for Pearl and for Jeffrey). Moreover, it is shown that Jeffrey's update rule arises via variational inference. In terms of categorical probability theory, this amounts to an analysis of the situation in terms of the behaviour of the multiset functor, extended to the Kleisli category of the distribution monad.

Causal Inference by String Diagram Surgery

Extracting causal relationships from observed correlations is a growing area in probabilistic reasoning, originating with the seminal work of Pearl and others from the early 1990s. This paper develops a new, categorically oriented view based on a clear distinction between syntax (string diagrams) and semantics (stochastic matrices), connected via interpretations as structure-preserving functors. A key notion in the identification of causal effects is that of an intervention, whereby a variable is forcefully set to a particular value independent of any prior propensities. We represent the effect of such an intervention as an endofunctor which performs `string diagram surgery' within the syntactic category of string diagrams. This diagram surgery in turn yields a new, interventional distribution via the interpretation functor. While in general there is no way to compute interventional distributions purely from observed data, we show that this is possible in certain special cases using a calculational tool called comb disintegration. We demonstrate the use of this technique on a well-known toy example, where we predict the causal effect of smoking on cancer in the presence of a confounding common cause. After developing this specific example, we show this technique provides simple sufficient conditions for computing interventions which apply to a wide variety of situations considered in the causal inference literature.

Categorical Aspects of Parameter Learning

Parameter learning is the technique for obtaining the probabilistic parameters in conditional probability tables in Bayesian networks from tables with (observed) data --- where it is assumed that the underlying graphical structure is known. There are basically two ways of doing so, referred to as maximal likelihood estimation (MLE) and as Bayesian learning. This paper provides a categorical analysis of these two techniques and describes them in terms of basic properties of the multiset monad M, the distribution monad D and the Giry monad G. In essence, learning is about the reltionships between multisets (used for counting) on the one hand and probability distributions on the other. These relationsips will be described as suitable natural transformations.

A Mathematical Account of Soft Evidence, and of Jeffrey's `destructive' versus Pearl's `constructive' updating

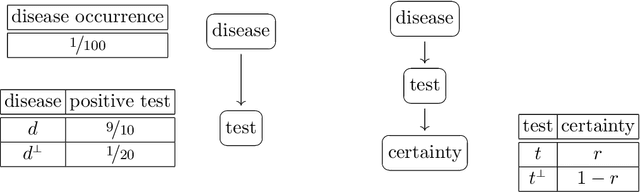
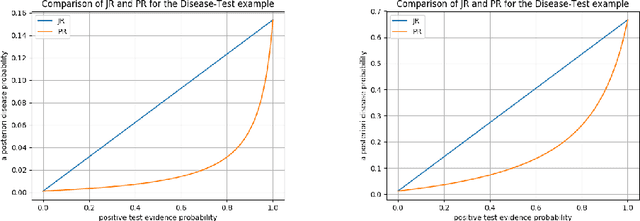
Evidence in probabilistic reasoning may be `hard' or `soft', that is, it may be of yes/no form, or it may involve a strength of belief, in the unit interval [0,1]. Reasoning with soft, $[0,1]$-valued evidence is important in many situations but may lead to different, confusing interpretations. This paper intends to bring more mathematical clarity to the field by shifting the existing focus from specification of soft evidence to accomodation of soft evidence. There are two main approaches, known as Jeffrey's rule and Pearl's method, which give different outcomes on soft evidence. This paper describes these two approaches as different ways of updating with soft evidence, highlighting their differences, similarities and applications. This account is based on a novel channel-based approach to Bayesian probability. Proper understanding of these two update mechanisms is highly relevant for inference, decision tools and probabilistic programming languages.

Disintegration and Bayesian Inversion via String Diagrams

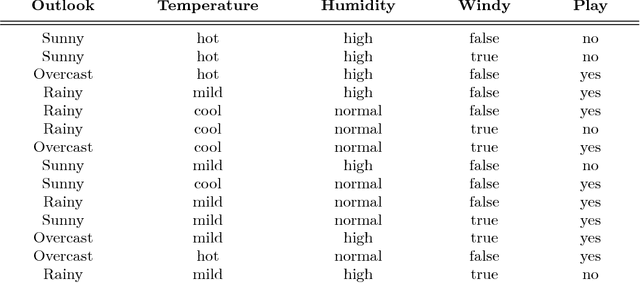
The notions of disintegration and Bayesian inversion are fundamental in conditional probability theory. They produce channels, as conditional probabilities, from a joint state, or from an already given channel (in opposite direction). These notions exist in the literature, in concrete situations, but are presented here in abstract graphical formulations. The resulting abstract descriptions are used for proving basic results in conditional probability theory. The existence of disintegration and Bayesian inversion is discussed for discrete probability, and also for measure-theoretic probability --- via standard Borel spaces and via likelihoods. Finally, the usefulness of disintegration and Bayesian inversion is illustrated in several examples.

The Logical Essentials of Bayesian Reasoning

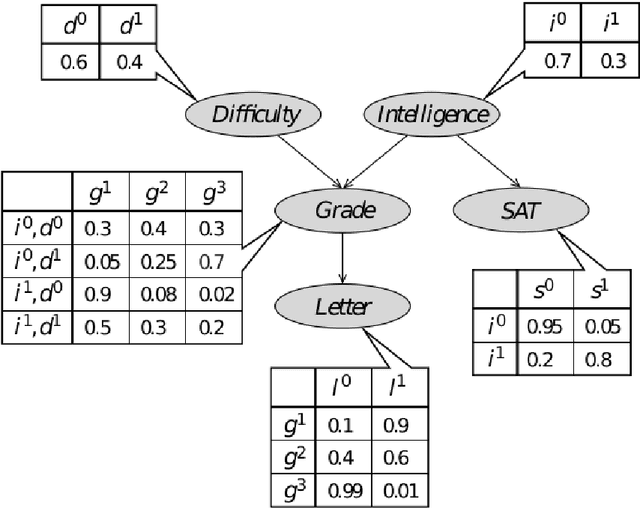
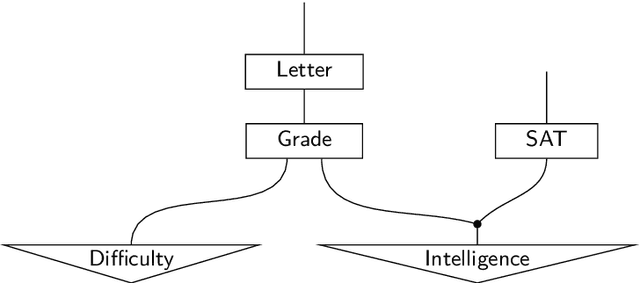
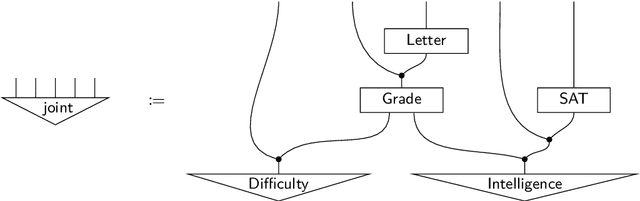
This chapter offers an accessible introduction to the channel-based approach to Bayesian probability theory. This framework rests on algebraic and logical foundations, inspired by the methodologies of programming language semantics. It offers a uniform, structured and expressive language for describing Bayesian phenomena in terms of familiar programming concepts, like channel, predicate transformation and state transformation. The introduction also covers inference in Bayesian networks, which will be modelled by a suitable calculus of string diagrams.

A Channel-based Exact Inference Algorithm for Bayesian Networks

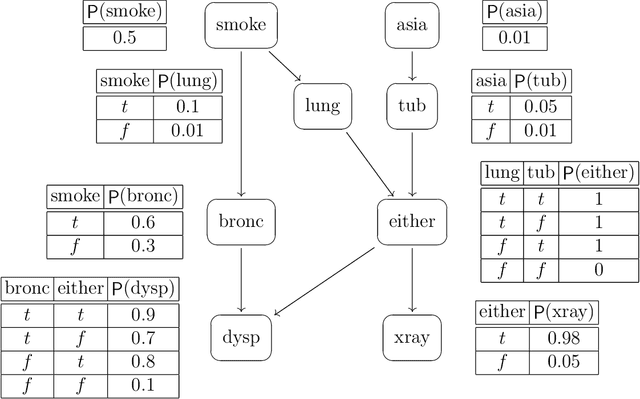
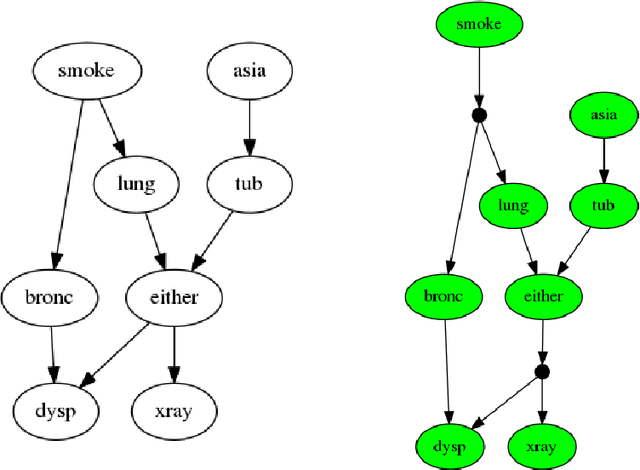
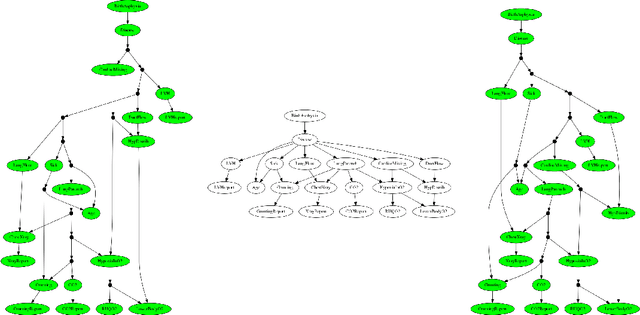
This paper describes a new algorithm for exact Bayesian inference that is based on a recently proposed compositional semantics of Bayesian networks in terms of channels. The paper concentrates on the ideas behind this algorithm, involving a linearisation (`stretching') of the Bayesian network, followed by a combination of forward state transformation and backward predicate transformation, while evidence is accumulated along the way. The performance of a prototype implementation of the algorithm in Python is briefly compared to a standard implementation (pgmpy): first results show competitive performance.

Neural Nets via Forward State Transformation and Backward Loss Transformation

This article studies (multilayer perceptron) neural networks with an emphasis on the transformations involved --- both forward and backward --- in order to develop a semantical/logical perspective that is in line with standard program semantics. The common two-pass neural network training algorithms make this viewpoint particularly fitting. In the forward direction, neural networks act as state transformers. In the reverse direction, however, neural networks change losses of outputs to losses of inputs, thereby acting like a (real-valued) predicate transformer. In this way, backpropagation is functorial by construction, as shown earlier in recent other work. We illustrate this perspective by training a simple instance of a neural network.