A Mathematical Account of Soft Evidence, and of Jeffrey's `destructive' versus Pearl's `constructive' updating

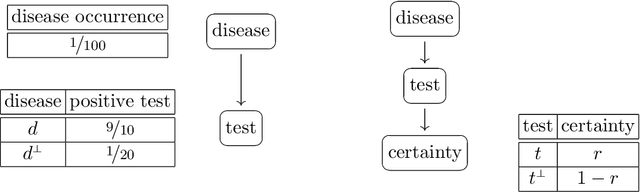
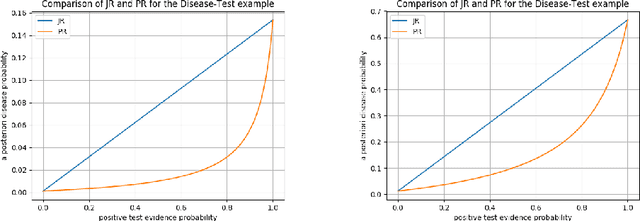
Evidence in probabilistic reasoning may be `hard' or `soft', that is, it may be of yes/no form, or it may involve a strength of belief, in the unit interval [0,1]. Reasoning with soft, $[0,1]$-valued evidence is important in many situations but may lead to different, confusing interpretations. This paper intends to bring more mathematical clarity to the field by shifting the existing focus from specification of soft evidence to accomodation of soft evidence. There are two main approaches, known as Jeffrey's rule and Pearl's method, which give different outcomes on soft evidence. This paper describes these two approaches as different ways of updating with soft evidence, highlighting their differences, similarities and applications. This account is based on a novel channel-based approach to Bayesian probability. Proper understanding of these two update mechanisms is highly relevant for inference, decision tools and probabilistic programming languages.