Control-Data Separation and Logical Condition Propagation for Efficient Inference on Probabilistic Programs

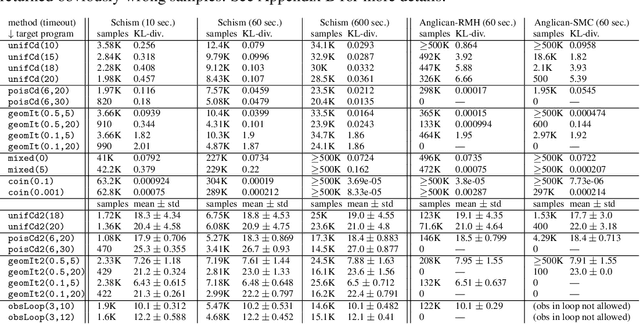
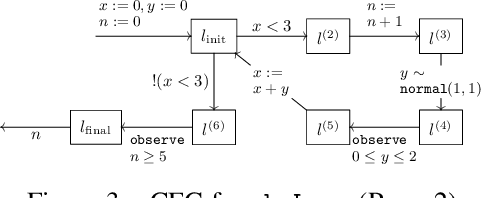
We introduce a novel sampling algorithm for Bayesian inference on imperative probabilistic programs. It features a hierarchical architecture that separates control flows from data: the top-level samples a control flow, and the bottom level samples data values along the control flow picked by the top level. This separation allows us to plug various language-based analysis techniques in probabilistic program sampling; specifically, we use logical backward propagation of observations for sampling efficiency. We implemented our algorithm on top of Anglican. The experimental results demonstrate our algorithm's efficiency, especially for programs with while loops and rare observations.

Disintegration and Bayesian Inversion via String Diagrams

The notions of disintegration and Bayesian inversion are fundamental in conditional probability theory. They produce channels, as conditional probabilities, from a joint state, or from an already given channel (in opposite direction). These notions exist in the literature, in concrete situations, but are presented here in abstract graphical formulations. The resulting abstract descriptions are used for proving basic results in conditional probability theory. The existence of disintegration and Bayesian inversion is discussed for discrete probability, and also for measure-theoretic probability --- via standard Borel spaces and via likelihoods. Finally, the usefulness of disintegration and Bayesian inversion is illustrated in several examples.