Continual Graph Learning: A Survey

Research on continual learning (CL) mainly focuses on data represented in the Euclidean space, while research on graph-structured data is scarce. Furthermore, most graph learning models are tailored for static graphs. However, graphs usually evolve continually in the real world. Catastrophic forgetting also emerges in graph learning models when being trained incrementally. This leads to the need to develop robust, effective and efficient continual graph learning approaches. Continual graph learning (CGL) is an emerging area aiming to realize continual learning on graph-structured data. This survey is written to shed light on this emerging area. It introduces the basic concepts of CGL and highlights two unique challenges brought by graphs. Then it reviews and categorizes recent state-of-the-art approaches, analyzing their strategies to tackle the unique challenges in CGL. Besides, it discusses the main concerns in each family of CGL methods, offering potential solutions. Finally, it explores the open issues and potential applications of CGL.

The Cause of Causal Emergence: Redistribution of Uncertainty

It is crucial to choose the appropriate scale in order to build an effective and informational representation of a complex system. Scientists carefully choose the scales for their experiments to extract the variables that describe the causalities in the system. They found that the coarse scale(macro) is sometimes more causal and informative than the numerous-parameter observations(micro). The phenomenon that the causality emerges by coarse-graining is called Causal Emergence(CE). Based on information theory, a number of recent works quantitatively showed that CE indeed happens while coarse-graining a micro model to the macro. However, the existing works have not discussed the question of why and when the CE happens. We quantitatively analyze the redistribution of uncertainties for coarse-graining and suggest that the redistribution of uncertainties is the cause of causal emergence. We further analyze the thresholds that determine if CE happens or not. From the regularity of the transition probability matrix(TPM) of discrete systems, the mathematical expressions of the model properties are derived. The values of thresholds for different operations are computed. The results provide the critical and specific conditions of CE as helpful suggestions for choosing the proper coarse-graining operation. The results also provided a new way to better understand the nature of causality and causal emergence.

Semi-Unsupervised Lifelong Learning for Sentiment Classification: Less Manual Data Annotation and More Self-Studying

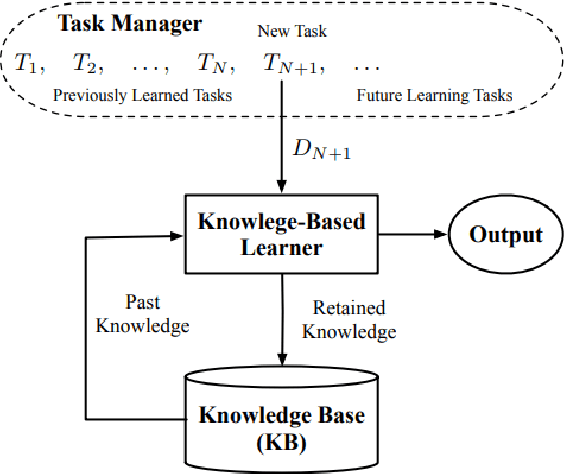
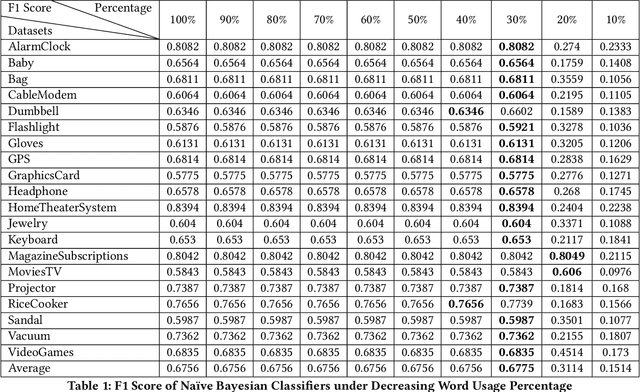
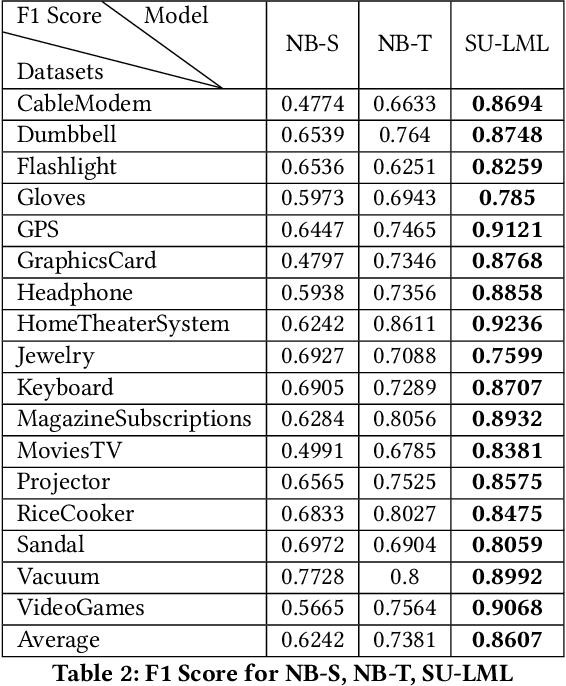
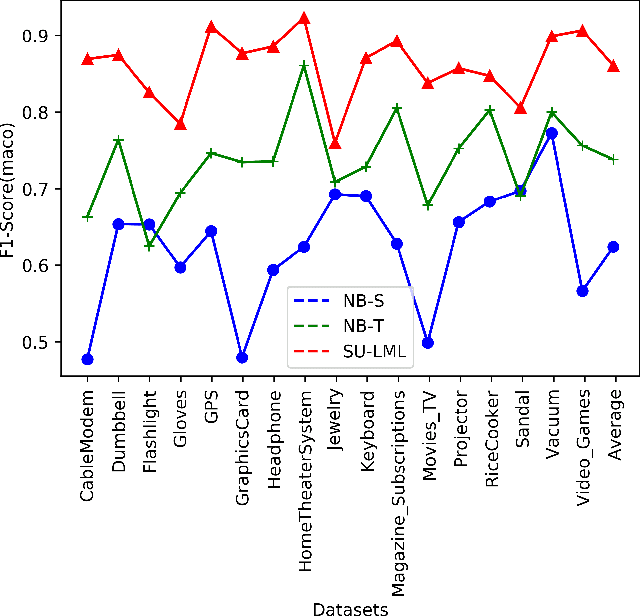
Lifelong machine learning is a novel machine learning paradigm which can continually accumulate knowledge during learning. The knowledge extracting and reusing abilities enable the lifelong machine learning to solve the related problems. The traditional approaches like Na\"ive Bayes and some neural network based approaches only aim to achieve the best performance upon a single task. Unlike them, the lifelong machine learning in this paper focuses on how to accumulate knowledge during learning and leverage them for further tasks. Meanwhile, the demand for labelled data for training also is significantly decreased with the knowledge reusing. This paper suggests that the aim of the lifelong learning is to use less labelled data and computational cost to achieve the performance as well as or even better than the supervised learning.