In-Hand Re-grasp Manipulation with Passive Dynamic Actions via Imitation Learning

Re-grasp manipulation leverages on ergonomic tools to assist humans in accomplishing diverse tasks. In certain scenarios, humans often employ external forces to effortlessly and precisely re-grasp tools like a hammer. Previous development on controllers for in-grasp sliding motion using passive dynamic actions (e.g.,gravity) relies on apprehension of finger-object contact information, and requires customized design for individual objects with varied geometry and weight distribution. It limits their adaptability to diverse objects. In this paper, we propose an end-to-end sliding motion controller based on imitation learning (IL) that necessitates minimal prior knowledge of object mechanics, relying solely on object position information. To expedite training convergence, we utilize a data glove to collect expert data trajectories and train the policy through Generative Adversarial Imitation Learning (GAIL). Simulation results demonstrate the controller's versatility in performing in-hand sliding tasks with objects of varying friction coefficients, geometric shapes, and masses. By migrating to a physical system using visual position estimation, the controller demonstrated an average success rate of 86%, surpassing the baseline algorithm's success rate of 35% of Behavior Cloning(BC) and 20% of Proximal Policy Optimization (PPO).

Eigen component analysis: A quantum theory incorporated machine learning technique to find linearly maximum separable components

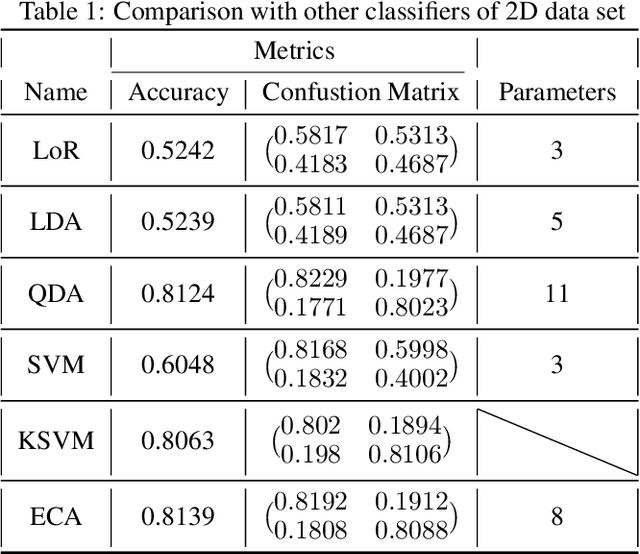
For a linear system, the response to a stimulus is often superposed by its responses to other decomposed stimuli. In quantum mechanics, a state is the superposition of multiple eigenstates. Here, by taking advantage of the phase difference, a common feature as we identified in data sets, we propose eigen component analysis (ECA), an interpretable linear learning model that incorporates the principle of quantum mechanics into the design of algorithm design for feature extraction, classification, dictionary and deep learning, and adversarial generation, etc. The simulation of ECA, possessing a measurable $class\text{-}label$ $\mathcal{H}$, on a classical computer outperforms the existing classical linear models. Eigen component analysis network (ECAN), a network of concatenated ECA models, enhances ECA and gains the potential to be not only integrated with nonlinear models, but also an interface for deep neural networks to implement on a quantum computer, by analogizing a data set as recordings of quantum states. Therefore, ECA and ECAN promise to expand the feasibility of linear learning models, by adopting the strategy of quantum machine learning to replace heavy nonlinear models with succinct linear operations in tackling complexity.