Eigen component analysis: A quantum theory incorporated machine learning technique to find linearly maximum separable components
Paper and Code
Apr 03, 2020
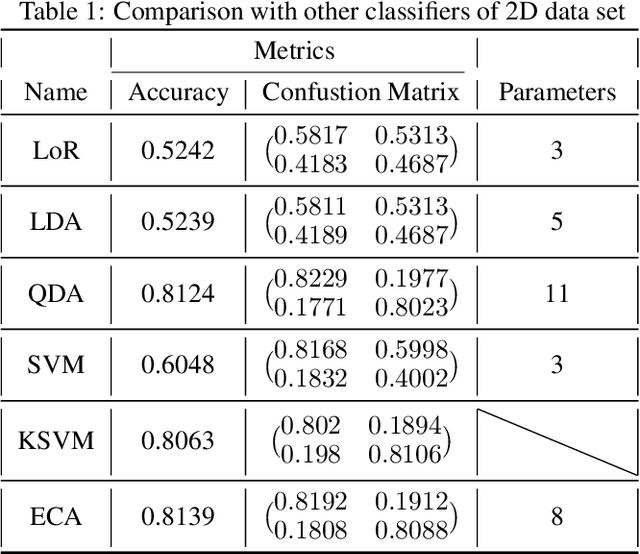


For a linear system, the response to a stimulus is often superposed by its responses to other decomposed stimuli. In quantum mechanics, a state is the superposition of multiple eigenstates. Here, by taking advantage of the phase difference, a common feature as we identified in data sets, we propose eigen component analysis (ECA), an interpretable linear learning model that incorporates the principle of quantum mechanics into the design of algorithm design for feature extraction, classification, dictionary and deep learning, and adversarial generation, etc. The simulation of ECA, possessing a measurable $class\text{-}label$ $\mathcal{H}$, on a classical computer outperforms the existing classical linear models. Eigen component analysis network (ECAN), a network of concatenated ECA models, enhances ECA and gains the potential to be not only integrated with nonlinear models, but also an interface for deep neural networks to implement on a quantum computer, by analogizing a data set as recordings of quantum states. Therefore, ECA and ECAN promise to expand the feasibility of linear learning models, by adopting the strategy of quantum machine learning to replace heavy nonlinear models with succinct linear operations in tackling complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge