Shanbo Chu
Learning Numeral Embeddings
Jan 11, 2020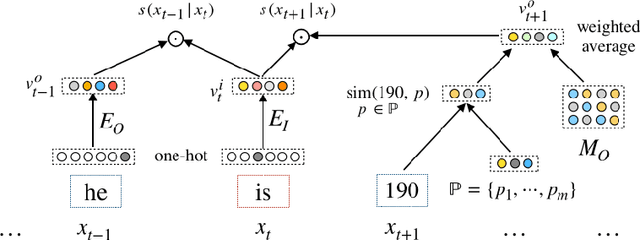

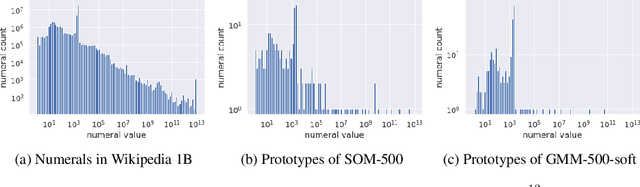
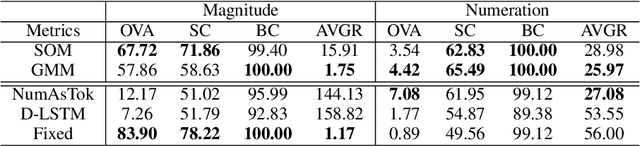
Abstract:Word embedding is an essential building block for deep learning methods for natural language processing. Although word embedding has been extensively studied over the years, the problem of how to effectively embed numerals, a special subset of words, is still underexplored. Existing word embedding methods do not learn numeral embeddings well because there are an infinite number of numerals and their individual appearances in training corpora are highly scarce. In this paper, we propose two novel numeral embedding methods that can handle the out-of-vocabulary (OOV) problem for numerals. We first induce a finite set of prototype numerals using either a self-organizing map or a Gaussian mixture model. We then represent the embedding of a numeral as a weighted average of the prototype number embeddings. Numeral embeddings represented in this manner can be plugged into existing word embedding learning approaches such as skip-gram for training. We evaluated our methods and showed its effectiveness on four intrinsic and extrinsic tasks: word similarity, embedding numeracy, numeral prediction, and sequence labeling.
Latent Dependency Forest Models
Nov 20, 2016



Abstract:Probabilistic modeling is one of the foundations of modern machine learning and artificial intelligence. In this paper, we propose a novel type of probabilistic models named latent dependency forest models (LDFMs). A LDFM models the dependencies between random variables with a forest structure that can change dynamically based on the variable values. It is therefore capable of modeling context-specific independence. We parameterize a LDFM using a first-order non-projective dependency grammar. Learning LDFMs from data can be formulated purely as a parameter learning problem, and hence the difficult problem of model structure learning is circumvented. Our experimental results show that LDFMs are competitive with existing probabilistic models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge