Distributed Multigrid Neural Solvers on Megavoxel Domains

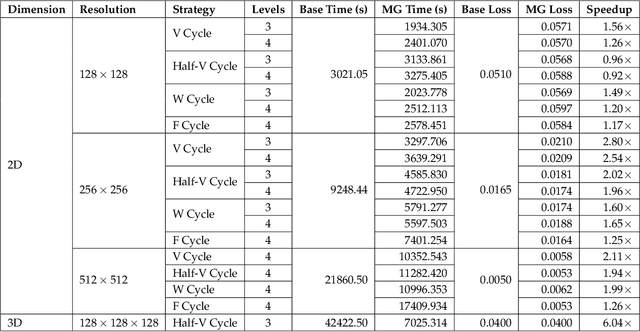
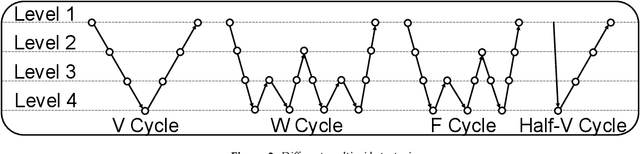
We consider the distributed training of large-scale neural networks that serve as PDE solvers producing full field outputs. We specifically consider neural solvers for the generalized 3D Poisson equation over megavoxel domains. A scalable framework is presented that integrates two distinct advances. First, we accelerate training a large model via a method analogous to the multigrid technique used in numerical linear algebra. Here, the network is trained using a hierarchy of increasing resolution inputs in sequence, analogous to the 'V', 'W', 'F', and 'Half-V' cycles used in multigrid approaches. In conjunction with the multi-grid approach, we implement a distributed deep learning framework which significantly reduces the time to solve. We show the scalability of this approach on both GPU (Azure VMs on Cloud) and CPU clusters (PSC Bridges2). This approach is deployed to train a generalized 3D Poisson solver that scales well to predict output full-field solutions up to the resolution of 512x512x512 for a high dimensional family of inputs.

Deep Generative Models that Solve PDEs: Distributed Computing for Training Large Data-Free Models

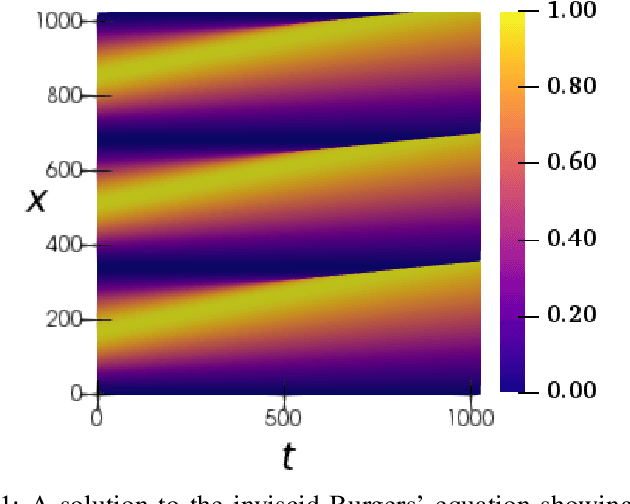
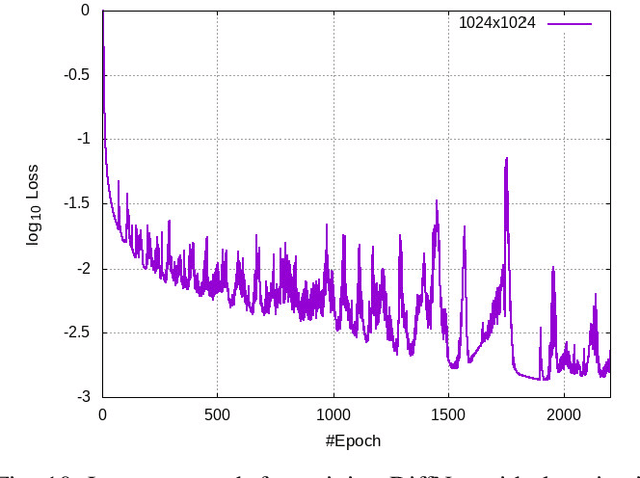
Recent progress in scientific machine learning (SciML) has opened up the possibility of training novel neural network architectures that solve complex partial differential equations (PDEs). Several (nearly data free) approaches have been recently reported that successfully solve PDEs, with examples including deep feed forward networks, generative networks, and deep encoder-decoder networks. However, practical adoption of these approaches is limited by the difficulty in training these models, especially to make predictions at large output resolutions ($\geq 1024 \times 1024$). Here we report on a software framework for data parallel distributed deep learning that resolves the twin challenges of training these large SciML models - training in reasonable time as well as distributing the storage requirements. Our framework provides several out of the box functionality including (a) loss integrity independent of number of processes, (b) synchronized batch normalization, and (c) distributed higher-order optimization methods. We show excellent scalability of this framework on both cloud as well as HPC clusters, and report on the interplay between bandwidth, network topology and bare metal vs cloud. We deploy this approach to train generative models of sizes hitherto not possible, showing that neural PDE solvers can be viably trained for practical applications. We also demonstrate that distributed higher-order optimization methods are $2-3\times$ faster than stochastic gradient-based methods and provide minimal convergence drift with higher batch-size.