Decentralized RL-Based Data Transmission Scheme for Energy Efficient Harvesting

The evolving landscape of the Internet of Things (IoT) has given rise to a pressing need for an efficient communication scheme. As the IoT user ecosystem continues to expand, traditional communication protocols grapple with substantial challenges in meeting its burgeoning demands, including energy consumption, scalability, data management, and interference. In response to this, the integration of wireless power transfer and data transmission has emerged as a promising solution. This paper considers an energy harvesting (EH)-oriented data transmission scheme, where a set of users are charged by their own multi-antenna power beacon (PB) and subsequently transmits data to a base station (BS) using an irregular slotted aloha (IRSA) channel access protocol. We propose a closed-form expression to model energy consumption for the present scheme, employing average channel state information (A-CSI) beamforming in the wireless power channel. Subsequently, we employ the reinforcement learning (RL) methodology, wherein every user functions as an agent tasked with the goal of uncovering their most effective strategy for replicating transmissions. This strategy is devised while factoring in their energy constraints and the maximum number of packets they need to transmit. Our results underscore the viability of this solution, particularly when the PB can be strategically positioned to ensure a strong line-of-sight connection with the user, highlighting the potential benefits of optimal deployment.

On learning parametric distributions from quantized samples

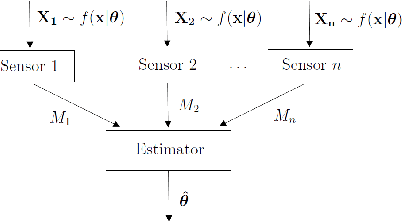
We consider the problem of learning parametric distributions from their quantized samples in a network. Specifically, $n$ agents or sensors observe independent samples of an unknown parametric distribution; and each of them uses $k$ bits to describe its observed sample to a central processor whose goal is to estimate the unknown distribution. First, we establish a generalization of the well-known van Trees inequality to general $L_p$-norms, with $p > 1$, in terms of Generalized Fisher information. Then, we develop minimax lower bounds on the estimation error for two losses: general $L_p$-norms and the related Wasserstein loss from optimal transport.