OPFData: Large-scale datasets for AC optimal power flow with topological perturbations

Solving the AC optimal power flow problem (AC-OPF) is critical to the efficient and safe planning and operation of power grids. Small efficiency improvements in this domain have the potential to lead to billions of dollars of cost savings, and significant reductions in emissions from fossil fuel generators. Recent work on data-driven solution methods for AC-OPF shows the potential for large speed improvements compared to traditional solvers; however, no large-scale open datasets for this problem exist. We present the largest readily-available collection of solved AC-OPF problems to date. This collection is orders of magnitude larger than existing readily-available datasets, allowing training of high-capacity data-driven models. Uniquely, it includes topological perturbations - a critical requirement for usage in realistic power grid operations. We hope this resource will spur the community to scale research to larger grid sizes with variable topology.

CANOS: A Fast and Scalable Neural AC-OPF Solver Robust To N-1 Perturbations

Optimal Power Flow (OPF) refers to a wide range of related optimization problems with the goal of operating power systems efficiently and securely. In the simplest setting, OPF determines how much power to generate in order to minimize costs while meeting demand for power and satisfying physical and operational constraints. In even the simplest case, power grid operators use approximations of the AC-OPF problem because solving the exact problem is prohibitively slow with state-of-the-art solvers. These approximations sacrifice accuracy and operational feasibility in favor of speed. This trade-off leads to costly "uplift payments" and increased carbon emissions, especially for large power grids. In the present work, we train a deep learning system (CANOS) to predict near-optimal solutions (within 1% of the true AC-OPF cost) without compromising speed (running in as little as 33--65 ms). Importantly, CANOS scales to realistic grid sizes with promising empirical results on grids containing as many as 10,000 buses. Finally, because CANOS is a Graph Neural Network, it is robust to changes in topology. We show that CANOS is accurate across N-1 topological perturbations of a base grid typically used in security-constrained analysis. This paves the way for more efficient optimization of more complex OPF problems which alter grid connectivity such as unit commitment, topology optimization and security-constrained OPF.

Expected Eligibility Traces

The question of how to determine which states and actions are responsible for a certain outcome is known as the credit assignment problem and remains a central research question in reinforcement learning and artificial intelligence. Eligibility traces enable efficient credit assignment to the recent sequence of states and actions experienced by the agent, but not to counterfactual sequences that could also have led to the current state. In this work, we introduce expected eligibility traces. Expected traces allow, with a single update, to update states and actions that could have preceded the current state, even if they did not do so on this occasion. We discuss when expected traces provide benefits over classic (instantaneous) traces in temporal-difference learning, and show that sometimes substantial improvements can be attained. We provide a way to smoothly interpolate between instantaneous and expected traces by a mechanism similar to bootstrapping, which ensures that the resulting algorithm is a strict generalisation of TD($\lambda$). Finally, we discuss possible extensions and connections to related ideas, such as successor features.

State2vec: Off-Policy Successor Features Approximators

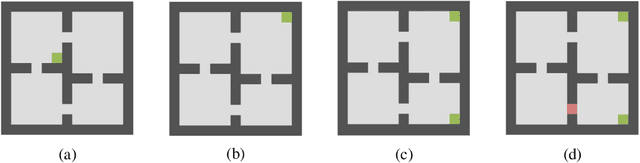
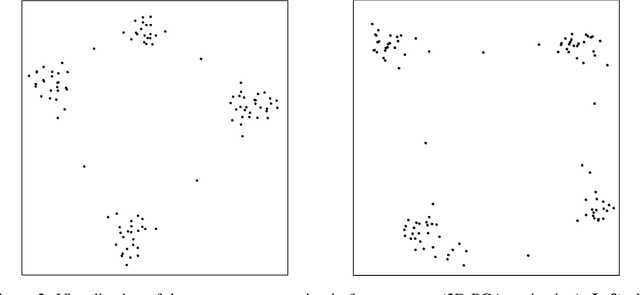
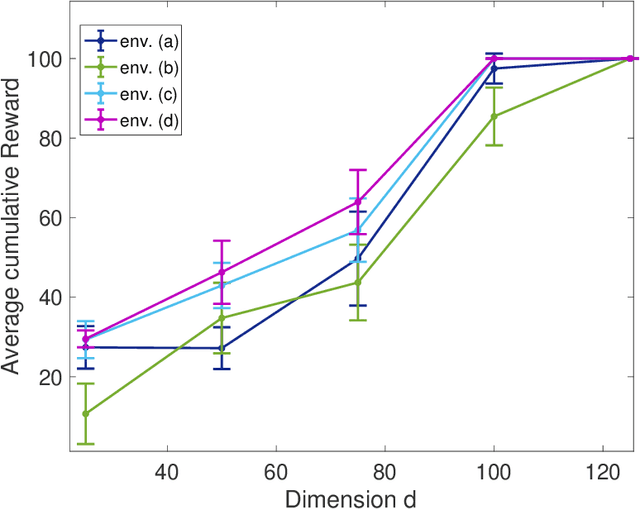
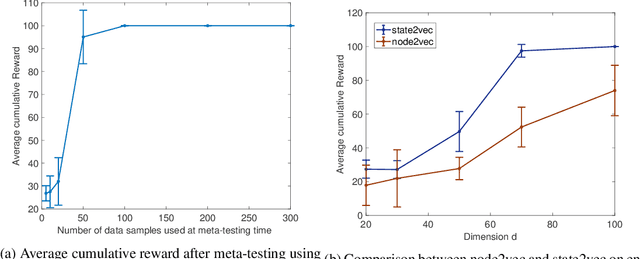
A major challenge in reinforcement learning (RL) is the design of agents that are able to generalize across tasks that share common dynamics. A viable solution is meta-reinforcement learning, which identifies common structures among past tasks to be then generalized to new tasks (meta-test). In meta-training, the RL agent learns state representations that encode prior information from a set of tasks, used to generalize the value function approximation. This has been proposed in the literature as successor representation approximators. While promising, these methods do not generalize well across optimal policies, leading to sampling-inefficiency during meta-test phases. In this paper, we propose state2vec, an efficient and low-complexity framework for learning successor features which (i) generalize across policies, (ii) ensure sample-efficiency during meta-test. We extend the well known node2vec framework to learn state embeddings that account for the discounted future state transitions in RL. The proposed off-policy state2vec captures the geometry of the underlying state space, making good basis functions for linear value function approximation.

Representation Learning on Graphs: A Reinforcement Learning Application

In this work, we study value function approximation in reinforcement learning (RL) problems with high dimensional state or action spaces via a generalized version of representation policy iteration (RPI). We consider the limitations of proto-value functions (PVFs) at accurately approximating the value function in low dimensions and we highlight the importance of features learning for an improved low-dimensional value function approximation. Then, we adopt different representation learning algorithm on graphs to learn the basis functions that best represent the value function. We empirically show that node2vec, an algorithm for scalable feature learning in networks, and the Variational Graph Auto-Encoder constantly outperform the commonly used smooth proto-value functions in low-dimensional feature space.