OPFData: Large-scale datasets for AC optimal power flow with topological perturbations

Solving the AC optimal power flow problem (AC-OPF) is critical to the efficient and safe planning and operation of power grids. Small efficiency improvements in this domain have the potential to lead to billions of dollars of cost savings, and significant reductions in emissions from fossil fuel generators. Recent work on data-driven solution methods for AC-OPF shows the potential for large speed improvements compared to traditional solvers; however, no large-scale open datasets for this problem exist. We present the largest readily-available collection of solved AC-OPF problems to date. This collection is orders of magnitude larger than existing readily-available datasets, allowing training of high-capacity data-driven models. Uniquely, it includes topological perturbations - a critical requirement for usage in realistic power grid operations. We hope this resource will spur the community to scale research to larger grid sizes with variable topology.

CANOS: A Fast and Scalable Neural AC-OPF Solver Robust To N-1 Perturbations

Optimal Power Flow (OPF) refers to a wide range of related optimization problems with the goal of operating power systems efficiently and securely. In the simplest setting, OPF determines how much power to generate in order to minimize costs while meeting demand for power and satisfying physical and operational constraints. In even the simplest case, power grid operators use approximations of the AC-OPF problem because solving the exact problem is prohibitively slow with state-of-the-art solvers. These approximations sacrifice accuracy and operational feasibility in favor of speed. This trade-off leads to costly "uplift payments" and increased carbon emissions, especially for large power grids. In the present work, we train a deep learning system (CANOS) to predict near-optimal solutions (within 1% of the true AC-OPF cost) without compromising speed (running in as little as 33--65 ms). Importantly, CANOS scales to realistic grid sizes with promising empirical results on grids containing as many as 10,000 buses. Finally, because CANOS is a Graph Neural Network, it is robust to changes in topology. We show that CANOS is accurate across N-1 topological perturbations of a base grid typically used in security-constrained analysis. This paves the way for more efficient optimization of more complex OPF problems which alter grid connectivity such as unit commitment, topology optimization and security-constrained OPF.

A General Stochastic Optimization Framework for Convergence Bidding

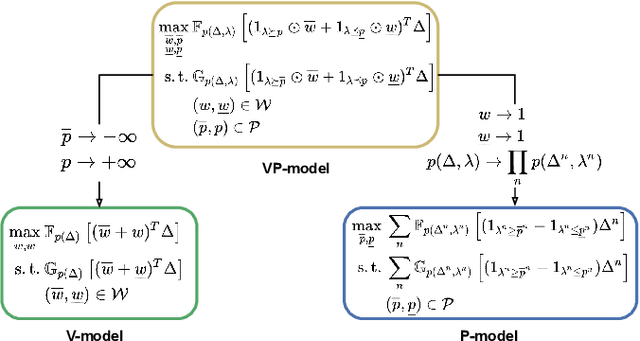
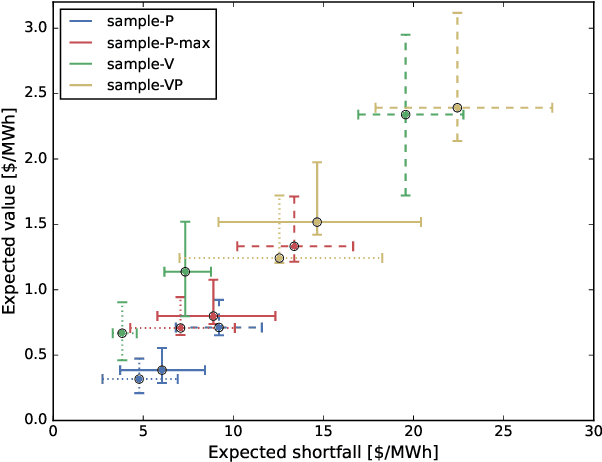
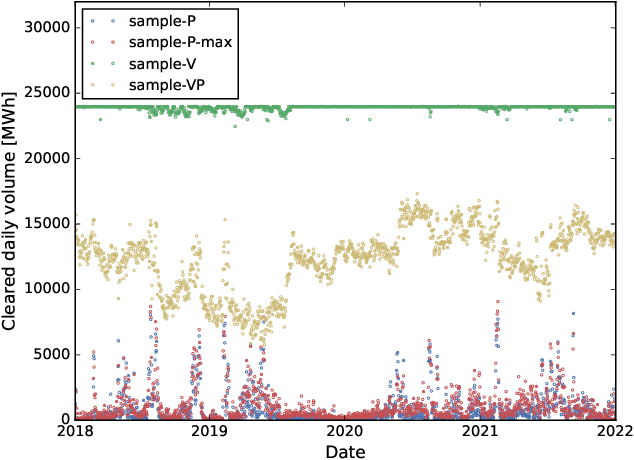
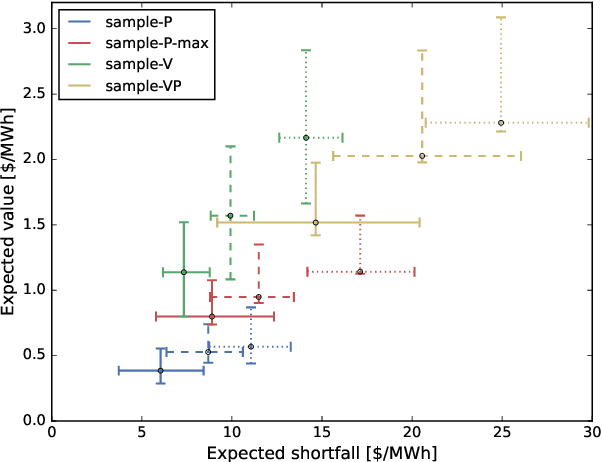
We introduce a general stochastic optimization framework to obtain optimal convergence (virtual) bid curves. Within this framework, we develop a computationally tractable linear programming-based optimization model, which produces bid prices and volumes simultaneously. We also show that different approximations and simplifications in the general model lead naturally to well-known convergence bidding approaches, such as self-scheduling and opportunistic approaches.