Frequency analysis and filter design for directed graphs with polar decomposition

In this study, we challenge the traditional approach of frequency analysis on directed graphs, which typically relies on a single measure of signal variation such as total variation. We argue that the inherent directionality in directed graphs necessitates a multifaceted analytical approach, one that incorporates multiple definitions of signal variations. Our methodology leverages the polar decomposition to define two distinct variations, each associated with different matrices derived from this decomposition. This approach not only provides a novel interpretation in the node domain but also reveals aspects of graph signals that may be overlooked with a singular measure of variation. Additionally, we develop graph filters specifically designed to smooth graph signals in accordance with our proposed variations. These filters allow for the bypassing of costly filtering operations associated with the original graph through effective cascading. We demonstrate the efficacy of our methodology using an M-block cyclic graph example, thereby validating our claims and showcasing the advantages of our multifaceted approach in analyzing signals on directed graphs.

Predicting traffic signals on transportation networks using spatio-temporal correlations on graphs

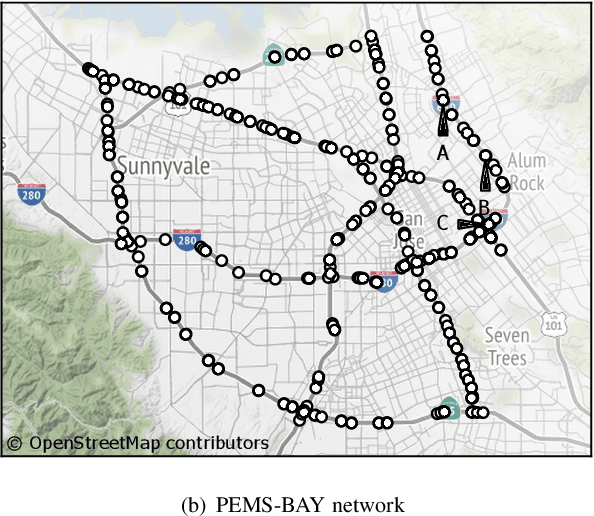
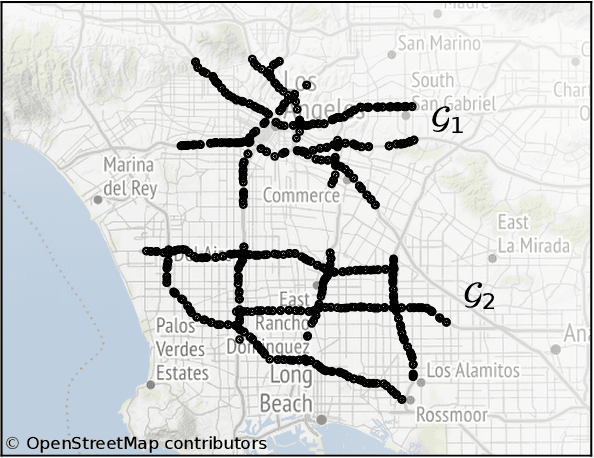
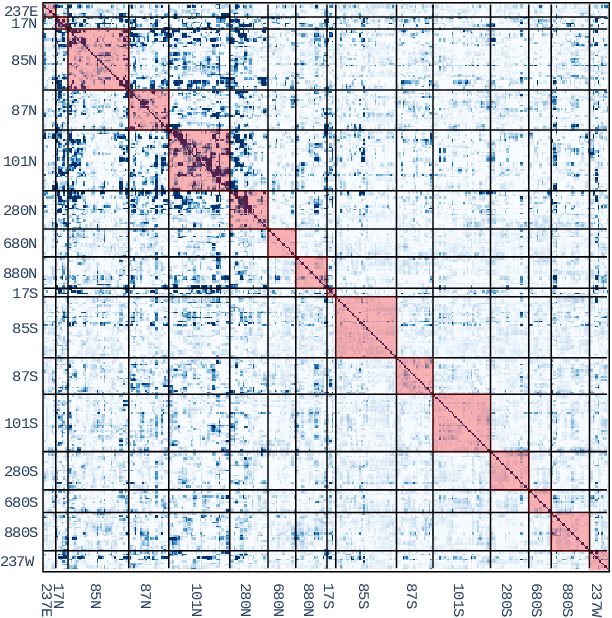
Forecasting multivariate time series is challenging as the variables are intertwined in time and space, like in the case of traffic signals. Defining signals on graphs relaxes such complexities by representing the evolution of signals over a space using relevant graph kernels such as the heat diffusion kernel. However, this kernel alone does not fully capture the actual dynamics of the data as it only relies on the graph structure. The gap can be filled by combining the graph kernel representation with data-driven models that utilize historical data. This paper proposes a traffic propagation model that merges multiple heat diffusion kernels into a data-driven prediction model to forecast traffic signals. We optimize the model parameters using Bayesian inference to minimize the prediction errors and, consequently, determine the mixing ratio of the two approaches. Such mixing ratio strongly depends on training data size and data anomalies, which typically correspond to the peak hours for traffic data. The proposed model demonstrates prediction accuracy comparable to that of the state-of-the-art deep neural networks with lower computational effort. It particularly shows excellent performance for long-term prediction since it inherits the data-driven models' periodicity modeling.

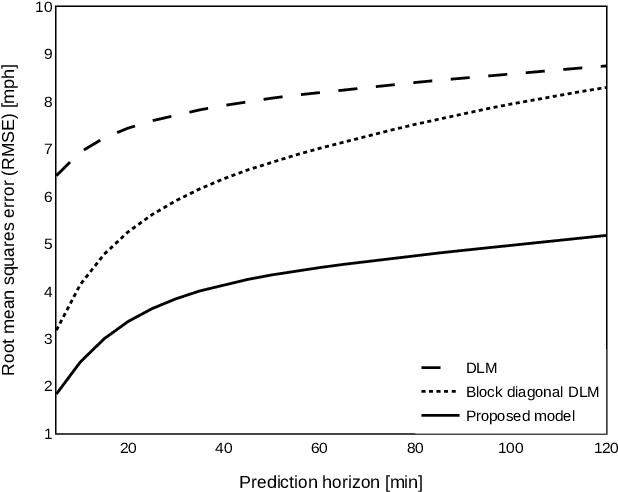
Travel time prediction for congested freeways with a dynamic linear model

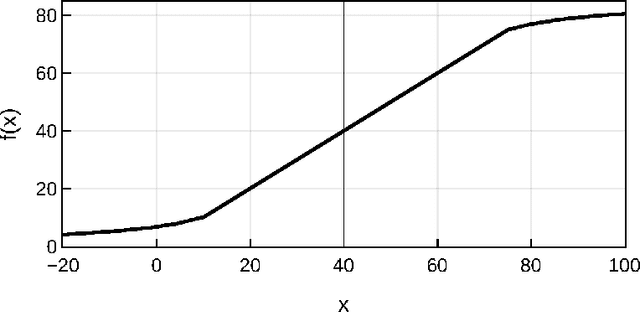
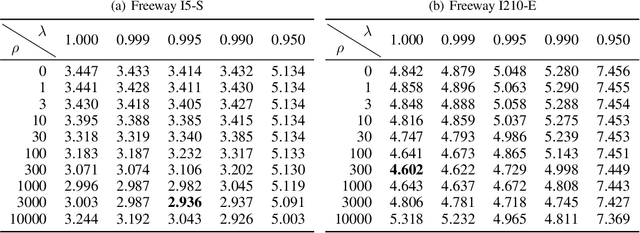
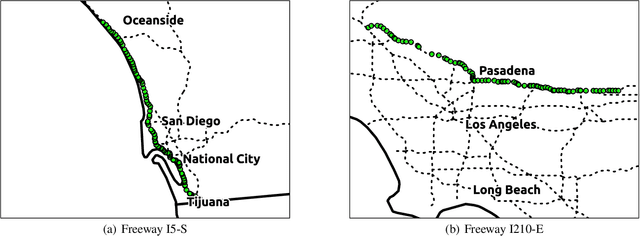
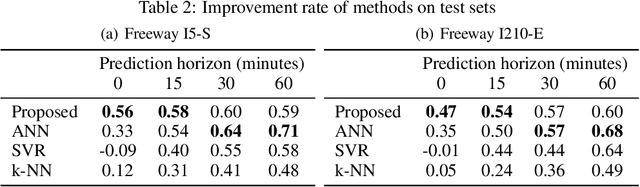
Accurate prediction of travel time is an essential feature to support Intelligent Transportation Systems (ITS). The non-linearity of traffic states, however, makes this prediction a challenging task. Here we propose to use dynamic linear models (DLMs) to approximate the non-linear traffic states. Unlike a static linear regression model, the DLMs assume that their parameters are changing across time. We design a DLM with model parameters defined at each time unit to describe the spatio-temporal characteristics of time-series traffic data. Based on our DLM and its model parameters analytically trained using historical data, we suggest an optimal linear predictor in the minimum mean square error (MMSE) sense. We compare our prediction accuracy of travel time for freeways in California (I210-E and I5-S) under highly congested traffic conditions with those of other methods: the instantaneous travel time, k-nearest neighbor, support vector regression, and artificial neural network. We show significant improvements in the accuracy, especially for short-term prediction.