Predicting traffic signals on transportation networks using spatio-temporal correlations on graphs

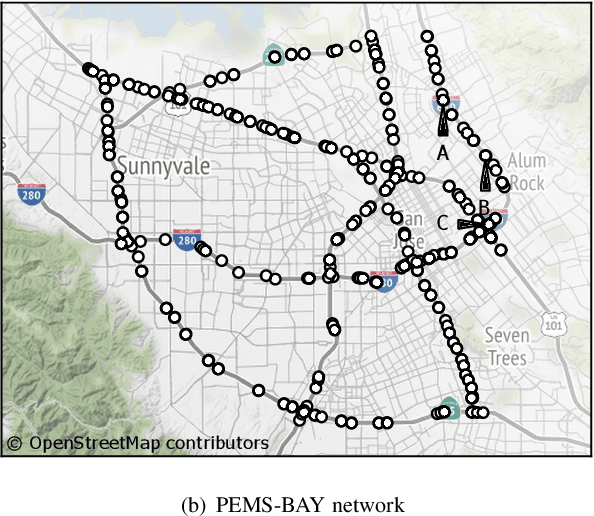
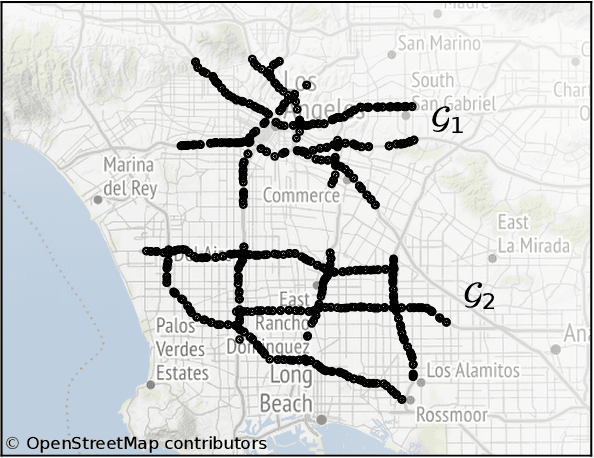
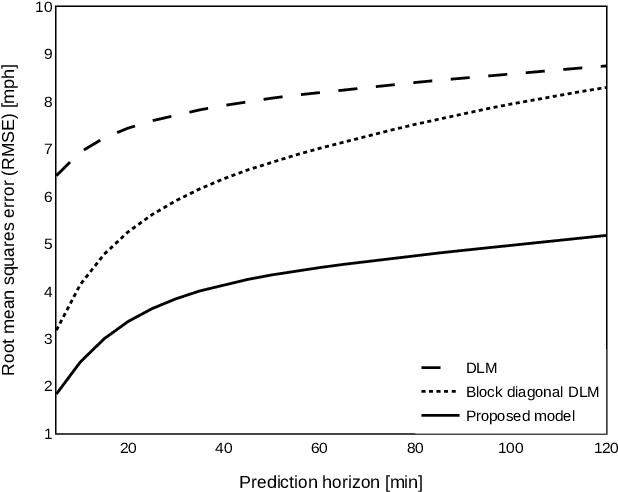
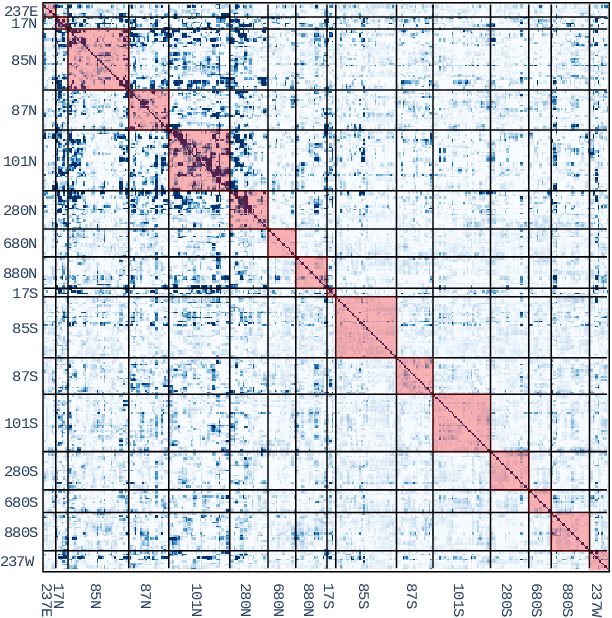
Forecasting multivariate time series is challenging as the variables are intertwined in time and space, like in the case of traffic signals. Defining signals on graphs relaxes such complexities by representing the evolution of signals over a space using relevant graph kernels such as the heat diffusion kernel. However, this kernel alone does not fully capture the actual dynamics of the data as it only relies on the graph structure. The gap can be filled by combining the graph kernel representation with data-driven models that utilize historical data. This paper proposes a traffic propagation model that merges multiple heat diffusion kernels into a data-driven prediction model to forecast traffic signals. We optimize the model parameters using Bayesian inference to minimize the prediction errors and, consequently, determine the mixing ratio of the two approaches. Such mixing ratio strongly depends on training data size and data anomalies, which typically correspond to the peak hours for traffic data. The proposed model demonstrates prediction accuracy comparable to that of the state-of-the-art deep neural networks with lower computational effort. It particularly shows excellent performance for long-term prediction since it inherits the data-driven models' periodicity modeling.