Frequency analysis and filter design for directed graphs with polar decomposition

In this study, we challenge the traditional approach of frequency analysis on directed graphs, which typically relies on a single measure of signal variation such as total variation. We argue that the inherent directionality in directed graphs necessitates a multifaceted analytical approach, one that incorporates multiple definitions of signal variations. Our methodology leverages the polar decomposition to define two distinct variations, each associated with different matrices derived from this decomposition. This approach not only provides a novel interpretation in the node domain but also reveals aspects of graph signals that may be overlooked with a singular measure of variation. Additionally, we develop graph filters specifically designed to smooth graph signals in accordance with our proposed variations. These filters allow for the bypassing of costly filtering operations associated with the original graph through effective cascading. We demonstrate the efficacy of our methodology using an M-block cyclic graph example, thereby validating our claims and showcasing the advantages of our multifaceted approach in analyzing signals on directed graphs.

Signal Variation Metrics and Graph Fourier Transforms for Directed Graphs

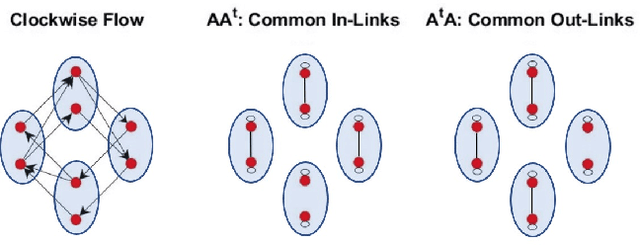
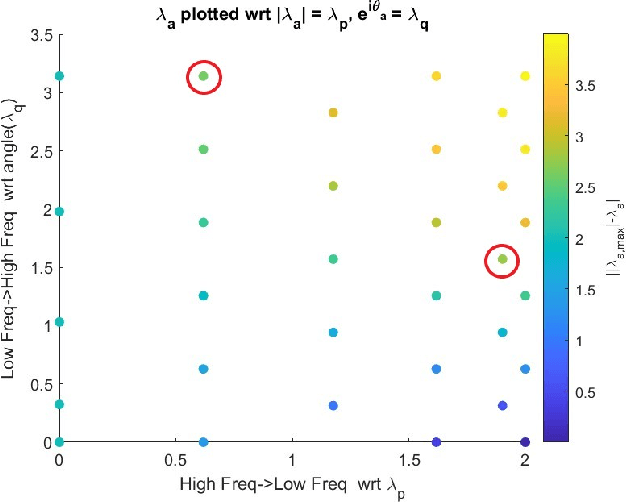
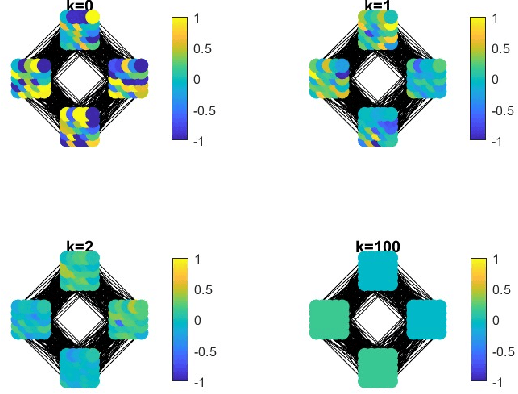
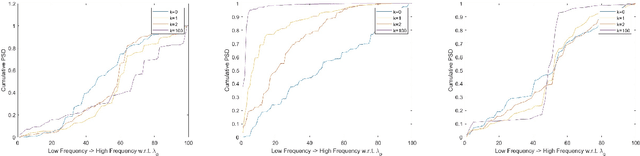
In this paper we consider the problem of constructing graph Fourier transforms (GFTs) for directed graphs (digraphs), with a focus on developing multiple GFT designs that can capture different types of variation over the digraph node-domain. Specifically, for any given digraph we propose three GFT designs based on the polar decomposition. Our method is closely related to existing polar decomposition based GFT designs, but with added interpretability in the digraph node-domain. Each of our proposed digraph GFTs has a clear node domain variation interpretation, so that one or more of the GFTs can be used to extract different insights from available graph signals. We demonstrate the benefits of our approach experimentally using M-block cyclic graphs, showing that the diffusion of signals on the graph leads to changes in the spectrum obtained from our proposed GFTs, but cannot be observed with the conventional GFT definition.