Guidance and Control Networks with Periodic Activation Functions

Inspired by the versatility of sinusoidal representation networks (SIRENs), we present a modified Guidance & Control Networks (G&CNETs) variant using periodic activation functions in the hidden layers. We demonstrate that the resulting G&CNETs train faster and achieve a lower overall training error on three different control scenarios on which G&CNETs have been tested previously. A preliminary analysis is presented in an attempt to explain the superior performance of the SIREN architecture for the particular types of tasks that G&CNETs excel on.

Closing the gap: Optimizing Guidance and Control Networks through Neural ODEs

We improve the accuracy of Guidance & Control Networks (G&CNETs), trained to represent the optimal control policies of a time-optimal transfer and a mass-optimal landing, respectively. In both cases we leverage the dynamics of the spacecraft, described by Ordinary Differential Equations which incorporate a neural network on their right-hand side (Neural ODEs). Since the neural dynamics is differentiable, the ODEs sensitivities to the network parameters can be computed using the variational equations, thereby allowing to update the G&CNET parameters based on the observed dynamics. We start with a straightforward regression task, training the G&CNETs on datasets of optimal trajectories using behavioural cloning. These networks are then refined using the Neural ODE sensitivities by minimizing the error between the final states and the target states. We demonstrate that for the orbital transfer, the final error to the target can be reduced by 99% on a single trajectory and by 70% on a batch of 500 trajectories. For the landing problem the reduction in error is around 98-99% (position) and 40-44% (velocity). This step significantly enhances the accuracy of G&CNETs, which instills greater confidence in their reliability for operational use. We also compare our results to the popular Dataset Aggregation method (DaGGER) and allude to the strengths and weaknesses of both methods.

Optimality Principles in Spacecraft Neural Guidance and Control

Spacecraft and drones aimed at exploring our solar system are designed to operate in conditions where the smart use of onboard resources is vital to the success or failure of the mission. Sensorimotor actions are thus often derived from high-level, quantifiable, optimality principles assigned to each task, utilizing consolidated tools in optimal control theory. The planned actions are derived on the ground and transferred onboard where controllers have the task of tracking the uploaded guidance profile. Here we argue that end-to-end neural guidance and control architectures (here called G&CNets) allow transferring onboard the burden of acting upon these optimality principles. In this way, the sensor information is transformed in real time into optimal plans thus increasing the mission autonomy and robustness. We discuss the main results obtained in training such neural architectures in simulation for interplanetary transfers, landings and close proximity operations, highlighting the successful learning of optimality principles by the neural model. We then suggest drone racing as an ideal gym environment to test these architectures on real robotic platforms, thus increasing confidence in their utilization on future space exploration missions. Drone racing shares with spacecraft missions both limited onboard computational capabilities and similar control structures induced from the optimality principle sought, but it also entails different levels of uncertainties and unmodelled effects. Furthermore, the success of G&CNets on extremely resource-restricted drones illustrates their potential to bring real-time optimal control within reach of a wider variety of robotic systems, both in space and on Earth.

Guidance & Control Networks for Time-Optimal Quadcopter Flight

Reaching fast and autonomous flight requires computationally efficient and robust algorithms. To this end, we train Guidance & Control Networks to approximate optimal control policies ranging from energy-optimal to time-optimal flight. We show that the policies become more difficult to learn the closer we get to the time-optimal 'bang-bang' control profile. We also assess the importance of knowing the maximum angular rotor velocity of the quadcopter and show that over- or underestimating this limit leads to less robust flight. We propose an algorithm to identify the current maximum angular rotor velocity onboard and a network that adapts its policy based on the identified limit. Finally, we extend previous work on Guidance & Control Networks by learning to take consecutive waypoints into account. We fly a 4x3m track in similar lap times as the differential-flatness-based minimum snap benchmark controller while benefiting from the flexibility that Guidance & Control Networks offer.

Neural representation of a time optimal, constant acceleration rendezvous

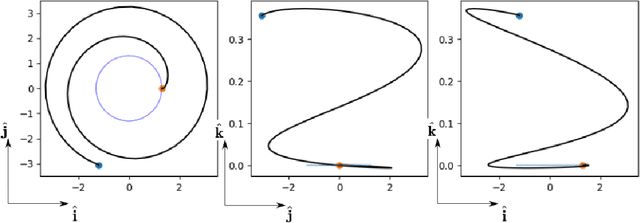
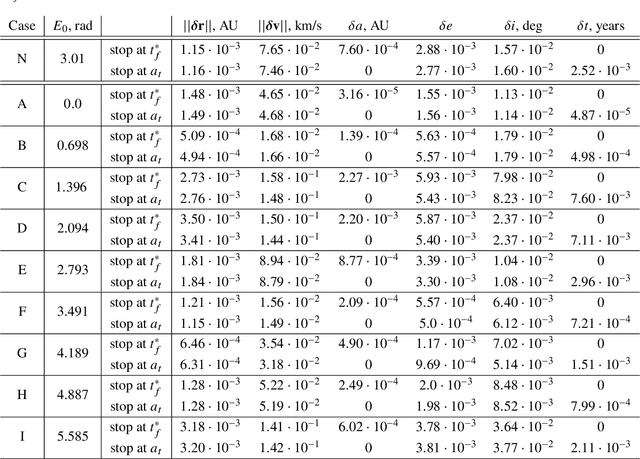
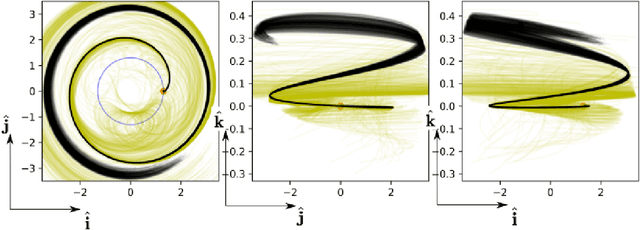
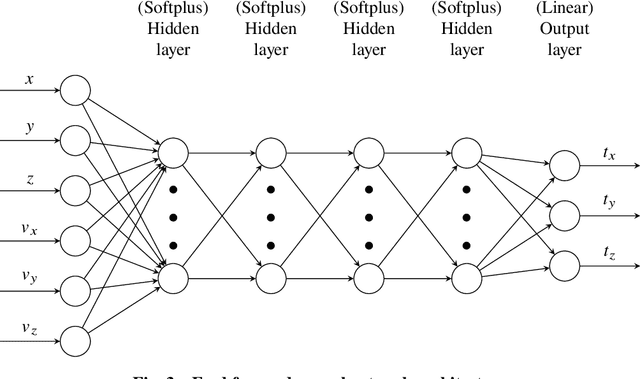
We train neural models to represent both the optimal policy (i.e. the optimal thrust direction) and the value function (i.e. the time of flight) for a time optimal, constant acceleration low-thrust rendezvous. In both cases we develop and make use of the data augmentation technique we call backward generation of optimal examples. We are thus able to produce and work with large dataset and to fully exploit the benefit of employing a deep learning framework. We achieve, in all cases, accuracies resulting in successful rendezvous (simulated following the learned policy) and time of flight predictions (using the learned value function). We find that residuals as small as a few m/s, thus well within the possibility of a spacecraft navigation $\Delta V$ budget, are achievable for the velocity at rendezvous. We also find that, on average, the absolute error to predict the optimal time of flight to rendezvous from any orbit in the asteroid belt to an Earth-like orbit is small (less than 4\%) and thus also of interest for practical uses, for example, during preliminary mission design phases.