AI-Powered Bayesian Inference

The advent of Generative Artificial Intelligence (GAI) has heralded an inflection point that changed how society thinks about knowledge acquisition. While GAI cannot be fully trusted for decision-making, it may still provide valuable information that can be integrated into a decision pipeline. Rather than seeing the lack of certitude and inherent randomness of GAI as a problem, we view it as an opportunity. Indeed, variable answers to given prompts can be leveraged to construct a prior distribution which reflects assuredness of AI predictions. This prior distribution may be combined with tailored datasets for a fully Bayesian analysis with an AI-driven prior. In this paper, we explore such a possibility within a non-parametric Bayesian framework. The basic idea consists of assigning a Dirichlet process prior distribution on the data-generating distribution with AI generative model as its baseline. Hyper-parameters of the prior can be tuned out-of-sample to assess the informativeness of the AI prior. Posterior simulation is achieved by computing a suitably randomized functional on an augmented data that consists of observed (labeled) data as well as fake data whose labels have been imputed using AI. This strategy can be parallelized and rapidly produces iid samples from the posterior by optimization as opposed to sampling from conditionals. Our method enables (predictive) inference and uncertainty quantification leveraging AI predictions in a coherent probabilistic manner.

Tree Bandits for Generative Bayes

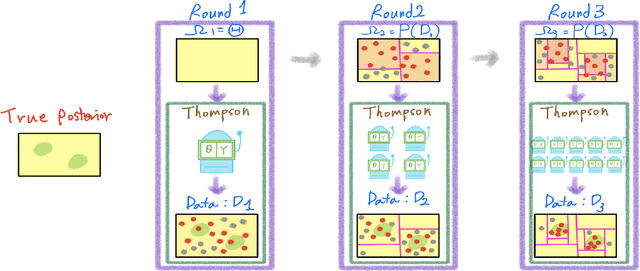
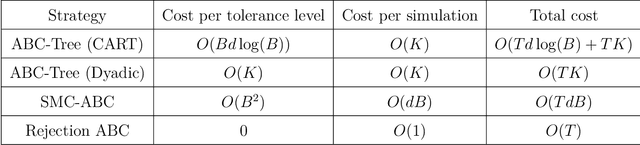
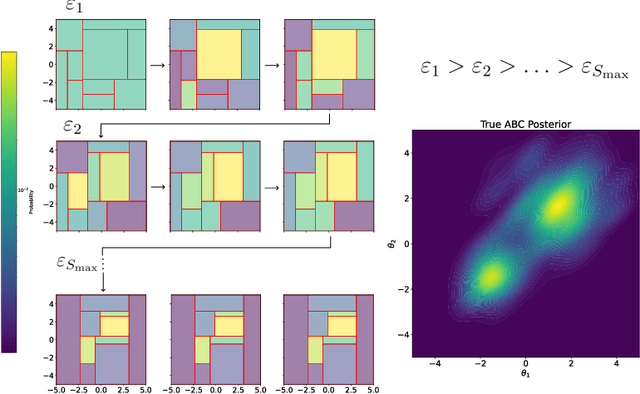
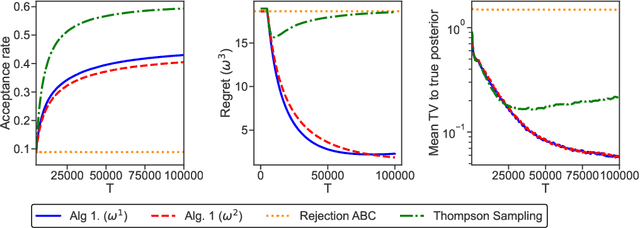
In generative models with obscured likelihood, Approximate Bayesian Computation (ABC) is often the tool of last resort for inference. However, ABC demands many prior parameter trials to keep only a small fraction that passes an acceptance test. To accelerate ABC rejection sampling, this paper develops a self-aware framework that learns from past trials and errors. We apply recursive partitioning classifiers on the ABC lookup table to sequentially refine high-likelihood regions into boxes. Each box is regarded as an arm in a binary bandit problem treating ABC acceptance as a reward. Each arm has a proclivity for being chosen for the next ABC evaluation, depending on the prior distribution and past rejections. The method places more splits in those areas where the likelihood resides, shying away from low-probability regions destined for ABC rejections. We provide two versions: (1) ABC-Tree for posterior sampling, and (2) ABC-MAP for maximum a posteriori estimation. We demonstrate accurate ABC approximability at much lower simulation cost. We justify the use of our tree-based bandit algorithms with nearly optimal regret bounds. Finally, we successfully apply our approach to the problem of masked image classification using deep generative models.

Measurement in the Age of LLMs: An Application to Ideological Scaling

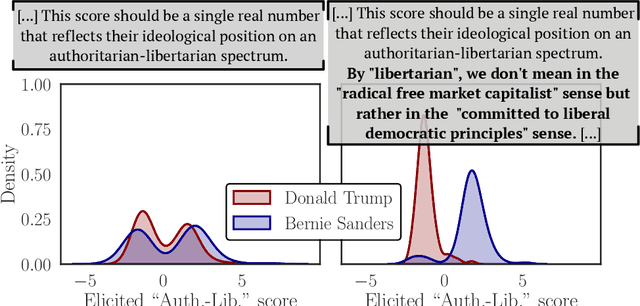
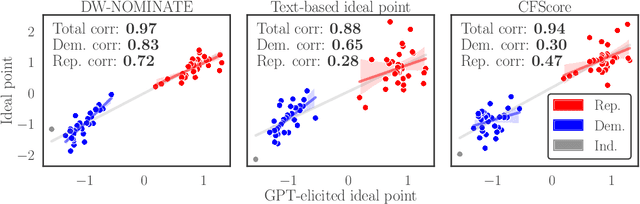
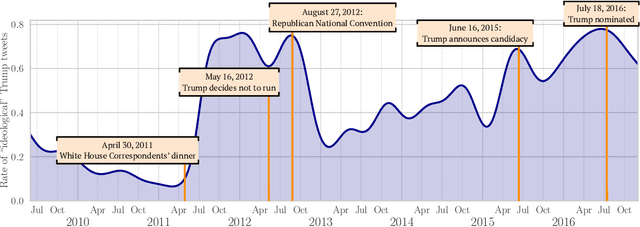
Much of social science is centered around terms like ``ideology'' or ``power'', which generally elude precise definition, and whose contextual meanings are trapped in surrounding language. This paper explores the use of large language models (LLMs) to flexibly navigate the conceptual clutter inherent to social scientific measurement tasks. We rely on LLMs' remarkable linguistic fluency to elicit ideological scales of both legislators and text, which accord closely to established methods and our own judgement. A key aspect of our approach is that we elicit such scores directly, instructing the LLM to furnish numeric scores itself. This approach affords a great deal of flexibility, which we showcase through a variety of different case studies. Our results suggest that LLMs can be used to characterize highly subtle and diffuse manifestations of political ideology in text.