Inverse Reinforcement Learning from Non-Stationary Learning Agents

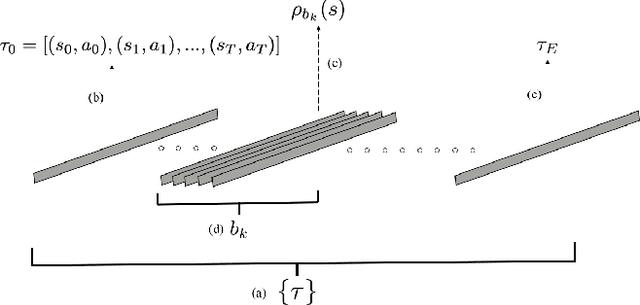
In this paper, we study an inverse reinforcement learning problem that involves learning the reward function of a learning agent using trajectory data collected while this agent is learning its optimal policy. To address this problem, we propose an inverse reinforcement learning method that allows us to estimate the policy parameters of the learning agent which can then be used to estimate its reward function. Our method relies on a new variant of the behavior cloning algorithm, which we call bundle behavior cloning, and uses a small number of trajectories generated by the learning agent's policy at different points in time to learn a set of policies that match the distribution of actions observed in the sampled trajectories. We then use the cloned policies to train a neural network model that estimates the reward function of the learning agent. We provide a theoretical analysis to show a complexity result on bound guarantees for our method that beats standard behavior cloning as well as numerical experiments for a reinforcement learning problem that validate the proposed method.

Transfer Reinforcement Learning in Heterogeneous Action Spaces using Subgoal Mapping

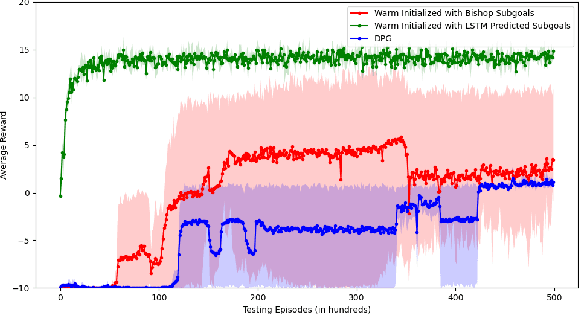
In this paper, we consider a transfer reinforcement learning problem involving agents with different action spaces. Specifically, for any new unseen task, the goal is to use a successful demonstration of this task by an expert agent in its action space to enable a learner agent learn an optimal policy in its own different action space with fewer samples than those required if the learner was learning on its own. Existing transfer learning methods across different action spaces either require handcrafted mappings between those action spaces provided by human experts, which can induce bias in the learning procedure, or require the expert agent to share its policy parameters with the learner agent, which does not generalize well to unseen tasks. In this work, we propose a method that learns a subgoal mapping between the expert agent policy and the learner agent policy. Since the expert agent and the learner agent have different action spaces, their optimal policies can have different subgoal trajectories. We learn this subgoal mapping by training a Long Short Term Memory (LSTM) network for a distribution of tasks and then use this mapping to predict the learner subgoal sequence for unseen tasks, thereby improving the speed of learning by biasing the agent's policy towards the predicted learner subgoal sequence. Through numerical experiments, we demonstrate that the proposed learning scheme can effectively find the subgoal mapping underlying the given distribution of tasks. Moreover, letting the learner agent imitate the expert agent's policy with the learnt subgoal mapping can significantly improve the sample efficiency and training time of the learner agent in unseen new tasks.

A Zeroth-Order Momentum Method for Risk-Averse Online Convex Games

We consider risk-averse learning in repeated unknown games where the goal of the agents is to minimize their individual risk of incurring significantly high cost. Specifically, the agents use the conditional value at risk (CVaR) as a risk measure and rely on bandit feedback in the form of the cost values of the selected actions at every episode to estimate their CVaR values and update their actions. A major challenge in using bandit feedback to estimate CVaR is that the agents can only access their own cost values, which, however, depend on the actions of all agents. To address this challenge, we propose a new risk-averse learning algorithm with momentum that utilizes the full historical information on the cost values. We show that this algorithm achieves sub-linear regret and matches the best known algorithms in the literature. We provide numerical experiments for a Cournot game that show that our method outperforms existing methods.