Scalable Deep Generative Relational Models with High-Order Node Dependence

We propose a probabilistic framework for modelling and exploring the latent structure of relational data. Given feature information for the nodes in a network, the scalable deep generative relational model (SDREM) builds a deep network architecture that can approximate potential nonlinear mappings between nodes' feature information and the nodes' latent representations. Our contribution is two-fold: (1) We incorporate high-order neighbourhood structure information to generate the latent representations at each node, which vary smoothly over the network. (2) Due to the Dirichlet random variable structure of the latent representations, we introduce a novel data augmentation trick which permits efficient Gibbs sampling. The SDREM can be used for large sparse networks as its computational cost scales with the number of positive links. We demonstrate its competitive performance through improved link prediction performance on a range of real-world datasets.

Binary Space Partitioning Forests

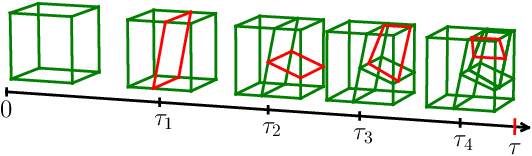
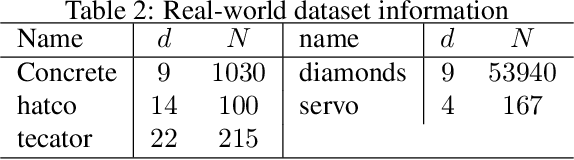
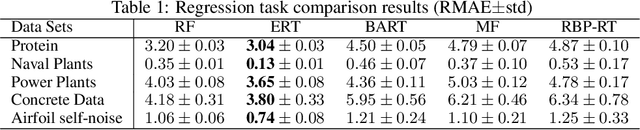
The Binary Space Partitioning~(BSP)-Tree process is proposed to produce flexible 2-D partition structures which are originally used as a Bayesian nonparametric prior for relational modelling. It can hardly be applied to other learning tasks such as regression trees because extending the BSP-Tree process to a higher dimensional space is nontrivial. This paper is the first attempt to extend the BSP-Tree process to a d-dimensional (d>2) space. We propose to generate a cutting hyperplane, which is assumed to be parallel to d-2 dimensions, to cut each node in the d-dimensional BSP-tree. By designing a subtle strategy to sample two free dimensions from d dimensions, the extended BSP-Tree process can inherit the essential self-consistency property from the original version. Based on the extended BSP-Tree process, an ensemble model, which is named the BSP-Forest, is further developed for regression tasks. Thanks to the retained self-consistency property, we can thus significantly reduce the geometric calculations in the inference stage. Compared to its counterpart, the Mondrian Forest, the BSP-Forest can achieve similar performance with fewer cuts due to its flexibility. The BSP-Forest also outperforms other (Bayesian) regression forests on a number of real-world data sets.

The Binary Space Partitioning-Tree Process

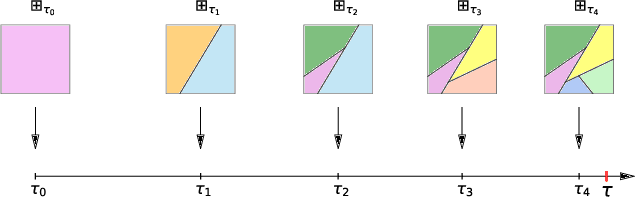
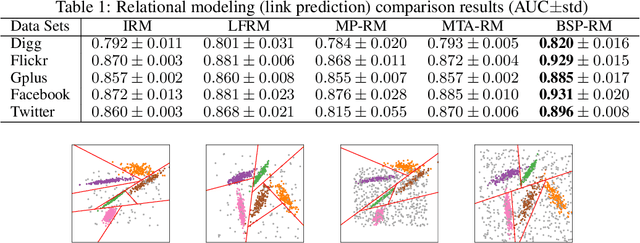
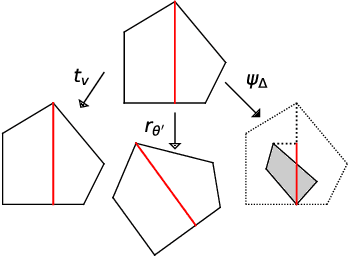
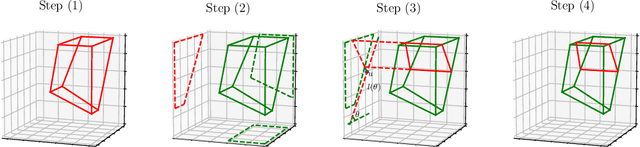
The Mondrian process represents an elegant and powerful approach for space partition modelling. However, as it restricts the partitions to be axis-aligned, its modelling flexibility is limited. In this work, we propose a self-consistent Binary Space Partitioning (BSP)-Tree process to generalize the Mondrian process. The BSP-Tree process is an almost surely right continuous Markov jump process that allows uniformly distributed oblique cuts in a two-dimensional convex polygon. The BSP-Tree process can also be extended using a non-uniform probability measure to generate direction differentiated cuts. The process is also self-consistent, maintaining distributional invariance under a restricted subdomain. We use Conditional-Sequential Monte Carlo for inference using the tree structure as the high-dimensional variable. The BSP-Tree process's performance on synthetic data partitioning and relational modelling demonstrates clear inferential improvements over the standard Mondrian process and other related methods.

Rectangular Bounding Process

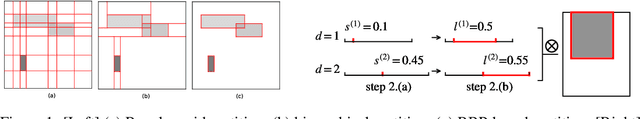
Stochastic partition models divide a multi-dimensional space into a number of rectangular regions, such that the data within each region exhibit certain types of homogeneity. Due to the nature of their partition strategy, existing partition models may create many unnecessary divisions in sparse regions when trying to describe data in dense regions. To avoid this problem we introduce a new parsimonious partition model -- the Rectangular Bounding Process (RBP) -- to efficiently partition multi-dimensional spaces, by employing a bounding strategy to enclose data points within rectangular bounding boxes. Unlike existing approaches, the RBP possesses several attractive theoretical properties that make it a powerful nonparametric partition prior on a hypercube. In particular, the RBP is self-consistent and as such can be directly extended from a finite hypercube to infinite (unbounded) space. We apply the RBP to regression trees and relational models as a flexible partition prior. The experimental results validate the merit of the RBP {in rich yet parsimonious expressiveness} compared to the state-of-the-art methods.