Rectangular Bounding Process
Paper and Code
Mar 10, 2019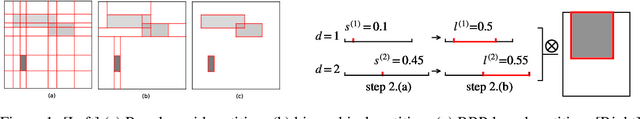
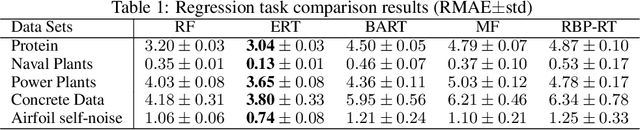


Stochastic partition models divide a multi-dimensional space into a number of rectangular regions, such that the data within each region exhibit certain types of homogeneity. Due to the nature of their partition strategy, existing partition models may create many unnecessary divisions in sparse regions when trying to describe data in dense regions. To avoid this problem we introduce a new parsimonious partition model -- the Rectangular Bounding Process (RBP) -- to efficiently partition multi-dimensional spaces, by employing a bounding strategy to enclose data points within rectangular bounding boxes. Unlike existing approaches, the RBP possesses several attractive theoretical properties that make it a powerful nonparametric partition prior on a hypercube. In particular, the RBP is self-consistent and as such can be directly extended from a finite hypercube to infinite (unbounded) space. We apply the RBP to regression trees and relational models as a flexible partition prior. The experimental results validate the merit of the RBP {in rich yet parsimonious expressiveness} compared to the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge