Binary Space Partitioning Forests

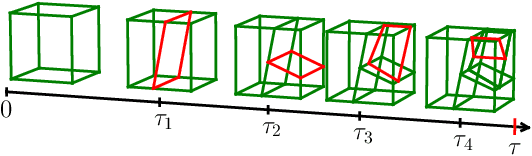
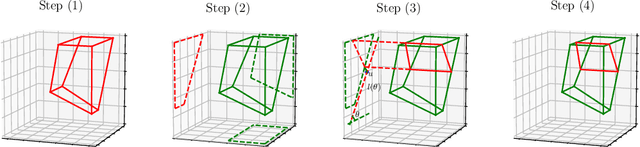
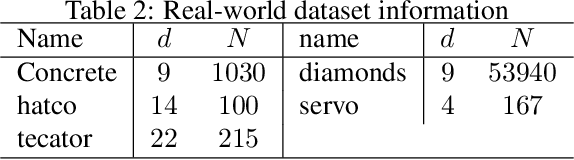
The Binary Space Partitioning~(BSP)-Tree process is proposed to produce flexible 2-D partition structures which are originally used as a Bayesian nonparametric prior for relational modelling. It can hardly be applied to other learning tasks such as regression trees because extending the BSP-Tree process to a higher dimensional space is nontrivial. This paper is the first attempt to extend the BSP-Tree process to a d-dimensional (d>2) space. We propose to generate a cutting hyperplane, which is assumed to be parallel to d-2 dimensions, to cut each node in the d-dimensional BSP-tree. By designing a subtle strategy to sample two free dimensions from d dimensions, the extended BSP-Tree process can inherit the essential self-consistency property from the original version. Based on the extended BSP-Tree process, an ensemble model, which is named the BSP-Forest, is further developed for regression tasks. Thanks to the retained self-consistency property, we can thus significantly reduce the geometric calculations in the inference stage. Compared to its counterpart, the Mondrian Forest, the BSP-Forest can achieve similar performance with fewer cuts due to its flexibility. The BSP-Forest also outperforms other (Bayesian) regression forests on a number of real-world data sets.