Saurav Basu
Effective Elastic Scaling of Deep Learning Workloads
Jun 24, 2020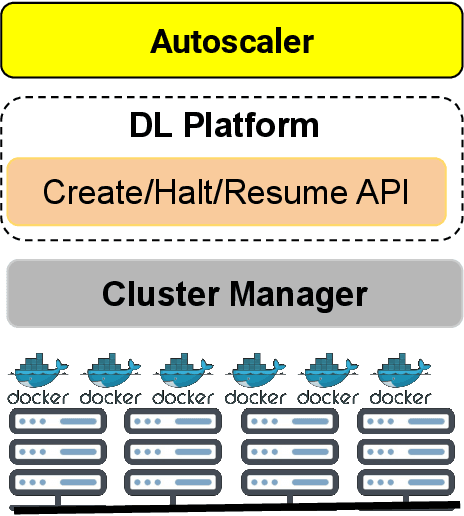
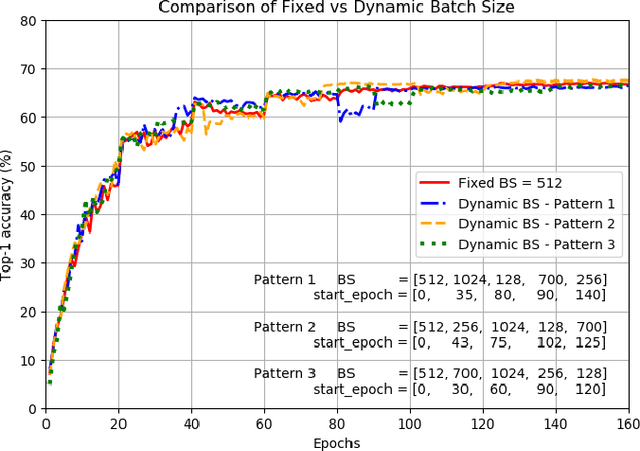
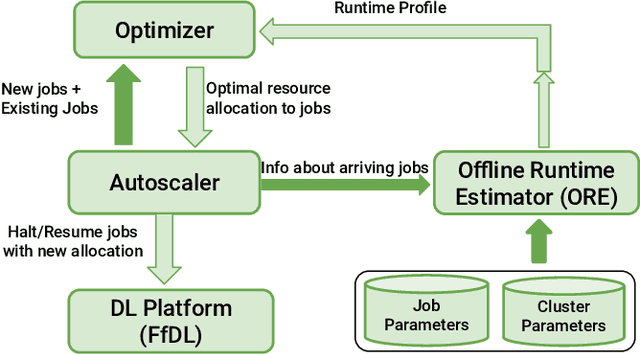

Abstract:The increased use of deep learning (DL) in academia, government and industry has, in turn, led to the popularity of on-premise and cloud-hosted deep learning platforms, whose goals are to enable organizations utilize expensive resources effectively, and to share said resources among multiple teams in a fair and effective manner. In this paper, we examine the elastic scaling of Deep Learning (DL) jobs over large-scale training platforms and propose a novel resource allocation strategy for DL training jobs, resulting in improved job run time performance as well as increased cluster utilization. We begin by analyzing DL workloads and exploit the fact that DL jobs can be run with a range of batch sizes without affecting their final accuracy. We formulate an optimization problem that explores a dynamic batch size allocation to individual DL jobs based on their scaling efficiency, when running on multiple nodes. We design a fast dynamic programming based optimizer to solve this problem in real-time to determine jobs that can be scaled up/down, and use this optimizer in an autoscaler to dynamically change the allocated resources and batch sizes of individual DL jobs. We demonstrate empirically that our elastic scaling algorithm can complete up to $\approx 2 \times$ as many jobs as compared to a strong baseline algorithm that also scales the number of GPUs but does not change the batch size. We also demonstrate that the average completion time with our algorithm is up to $\approx 10 \times$ faster than that of the baseline.
Layer Dynamics of Linearised Neural Nets
Apr 24, 2019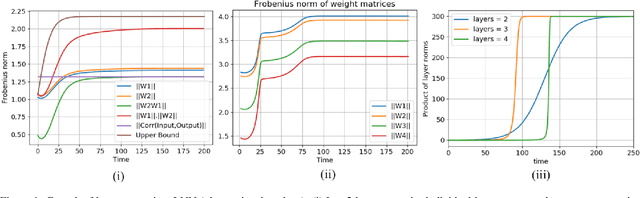
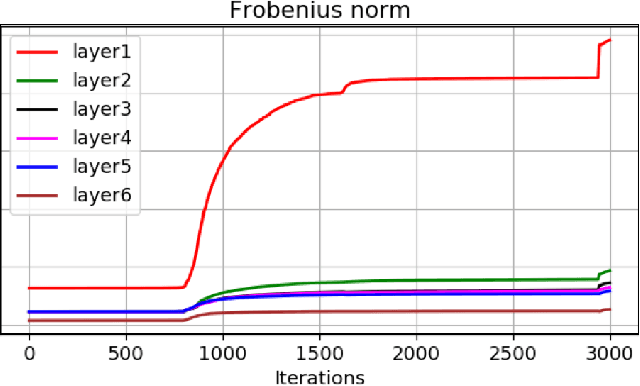
Abstract:Despite the phenomenal success of deep learning in recent years, there remains a gap in understanding the fundamental mechanics of neural nets. More research is focussed on handcrafting complex and larger networks, and the design decisions are often ad-hoc and based on intuition. Some recent research has aimed to demystify the learning dynamics in neural nets by attempting to build a theory from first principles, such as characterising the non-linear dynamics of specialised \textit{linear} deep neural nets (such as orthogonal networks). In this work, we expand and derive properties of learning dynamics respected by general multi-layer linear neural nets. Although an over-parameterisation of a single layer linear network, linear multi-layer neural nets offer interesting insights that explain how learning dynamics proceed in small pockets of the data space. We show in particular that multiple layers in linear nets grow at approximately the same rate, and there are distinct phases of learning with markedly different layer growth. We then apply a linearisation process to a general RelU neural net and show how nonlinearity breaks down the growth symmetry observed in liner neural nets. Overall, our work can be viewed as an initial step in building a theory for understanding the effect of layer design on the learning dynamics from first principles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge