Neuro-symbolic EDA-based Optimisation using ILP-enhanced DBNs

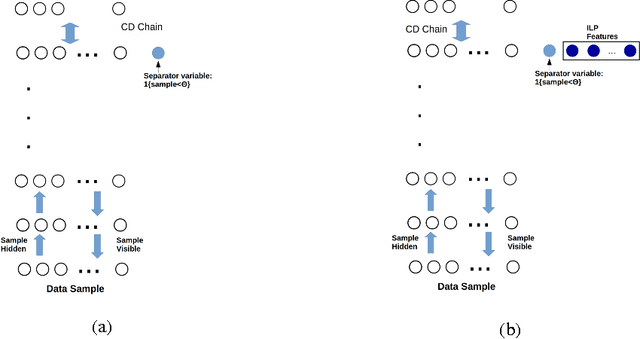
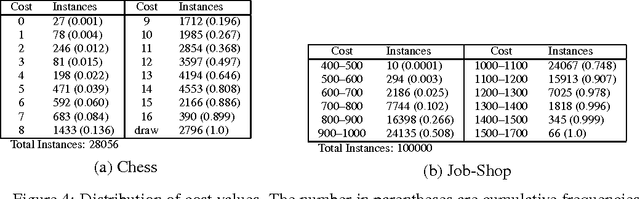
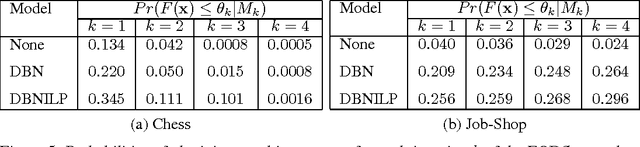
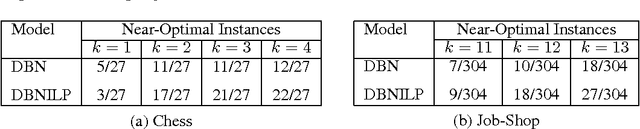
We investigate solving discrete optimisation problems using the estimation of distribution (EDA) approach via a novel combination of deep belief networks(DBN) and inductive logic programming (ILP).While DBNs are used to learn the structure of successively better feasible solutions,ILP enables the incorporation of domain-based background knowledge related to the goodness of solutions.Recent work showed that ILP could be an effective way to use domain knowledge in an EDA scenario.However,in a purely ILP-based EDA,sampling successive populations is either inefficient or not straightforward.In our Neuro-symbolic EDA,an ILP engine is used to construct a model for good solutions using domain-based background knowledge.These rules are introduced as Boolean features in the last hidden layer of DBNs used for EDA-based optimization.This incorporation of logical ILP features requires some changes while training and sampling from DBNs: (a)our DBNs need to be trained with data for units at the input layer as well as some units in an otherwise hidden layer, and (b)we would like the samples generated to be drawn from instances entailed by the logical model.We demonstrate the viability of our approach on instances of two optimisation problems: predicting optimal depth-of-win for the KRK endgame,and jobshop scheduling.Our results are promising: (i)On each iteration of distribution estimation,samples obtained with an ILP-assisted DBN have a substantially greater proportion of good solutions than samples generated using a DBN without ILP features, and (ii)On termination of distribution estimation,samples obtained using an ILP-assisted DBN contain more near-optimal samples than samples from a DBN without ILP features.These results suggest that the use of ILP-constructed theories could be useful for incorporating complex domain-knowledge into deep models for estimation of distribution based procedures.

Generation of Near-Optimal Solutions Using ILP-Guided Sampling

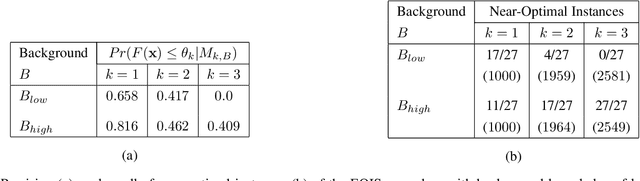
Our interest in this paper is in optimisation problems that are intractable to solve by direct numerical optimisation, but nevertheless have significant amounts of relevant domain-specific knowledge. The category of heuristic search techniques known as estimation of distribution algorithms (EDAs) seek to incrementally sample from probability distributions in which optimal (or near-optimal) solutions have increasingly higher probabilities. Can we use domain knowledge to assist the estimation of these distributions? To answer this in the affirmative, we need: (a)a general-purpose technique for the incorporation of domain knowledge when constructing models for optimal values; and (b)a way of using these models to generate new data samples. Here we investigate a combination of the use of Inductive Logic Programming (ILP) for (a), and standard logic-programming machinery to generate new samples for (b). Specifically, on each iteration of distribution estimation, an ILP engine is used to construct a model for good solutions. The resulting theory is then used to guide the generation of new data instances, which are now restricted to those derivable using the ILP model in conjunction with the background knowledge). We demonstrate the approach on two optimisation problems (predicting optimal depth-of-win for the KRK endgame, and job-shop scheduling). Our results are promising: (a)On each iteration of distribution estimation, samples obtained with an ILP theory have a substantially greater proportion of good solutions than samples without a theory; and (b)On termination of distribution estimation, samples obtained with an ILP theory contain more near-optimal samples than samples without a theory. Taken together, these results suggest that the use of ILP-constructed theories could be a useful technique for incorporating complex domain-knowledge into estimation distribution procedures.

Efficiently Discovering Frequent Motifs in Large-scale Sensor Data

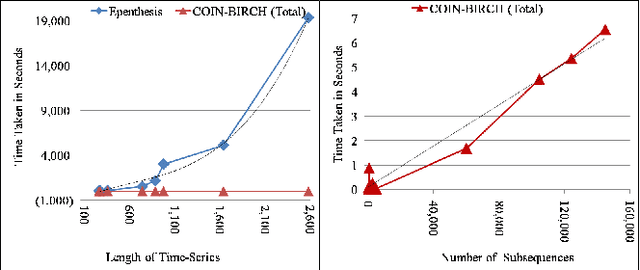
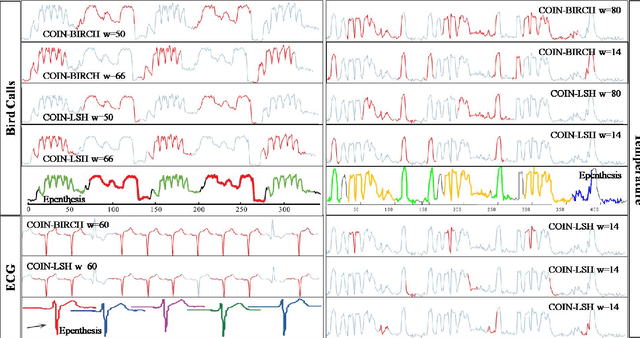
While analyzing vehicular sensor data, we found that frequently occurring waveforms could serve as features for further analysis, such as rule mining, classification, and anomaly detection. The discovery of waveform patterns, also known as time-series motifs, has been studied extensively; however, available techniques for discovering frequently occurring time-series motifs were found lacking in either efficiency or quality: Standard subsequence clustering results in poor quality, to the extent that it has even been termed 'meaningless'. Variants of hierarchical clustering using techniques for efficient discovery of 'exact pair motifs' find high-quality frequent motifs, but at the cost of high computational complexity, making such techniques unusable for our voluminous vehicular sensor data. We show that good quality frequent motifs can be discovered using bounded spherical clustering of time-series subsequences, which we refer to as COIN clustering, with near linear complexity in time-series size. COIN clustering addresses many of the challenges that previously led to subsequence clustering being viewed as meaningless. We describe an end-to-end motif-discovery procedure using a sequence of pre and post-processing techniques that remove trivial-matches and shifted-motifs, which also plagued previous subsequence-clustering approaches. We demonstrate that our technique efficiently discovers frequent motifs in voluminous vehicular sensor data as well as in publicly available data sets.