Richa Rawat
Neuro-symbolic EDA-based Optimisation using ILP-enhanced DBNs
Dec 20, 2016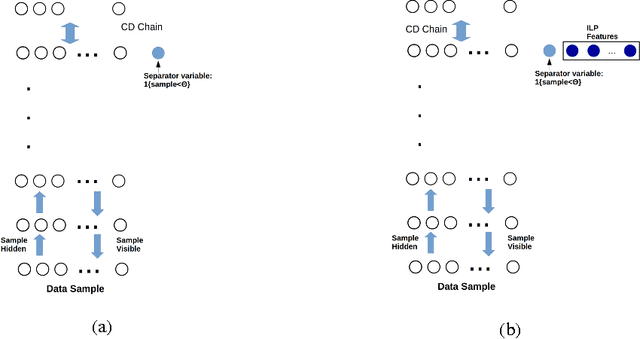
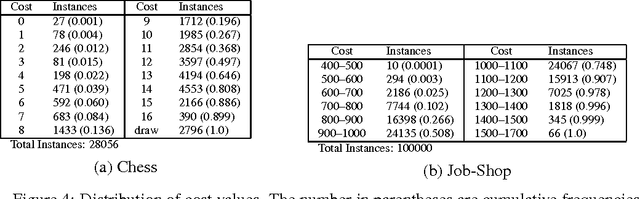
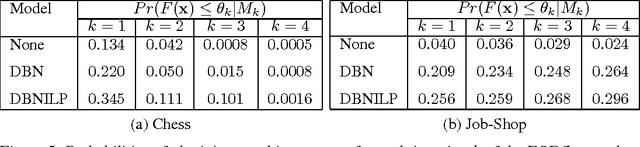
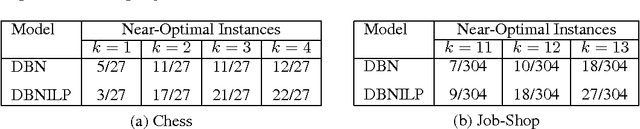
Abstract:We investigate solving discrete optimisation problems using the estimation of distribution (EDA) approach via a novel combination of deep belief networks(DBN) and inductive logic programming (ILP).While DBNs are used to learn the structure of successively better feasible solutions,ILP enables the incorporation of domain-based background knowledge related to the goodness of solutions.Recent work showed that ILP could be an effective way to use domain knowledge in an EDA scenario.However,in a purely ILP-based EDA,sampling successive populations is either inefficient or not straightforward.In our Neuro-symbolic EDA,an ILP engine is used to construct a model for good solutions using domain-based background knowledge.These rules are introduced as Boolean features in the last hidden layer of DBNs used for EDA-based optimization.This incorporation of logical ILP features requires some changes while training and sampling from DBNs: (a)our DBNs need to be trained with data for units at the input layer as well as some units in an otherwise hidden layer, and (b)we would like the samples generated to be drawn from instances entailed by the logical model.We demonstrate the viability of our approach on instances of two optimisation problems: predicting optimal depth-of-win for the KRK endgame,and jobshop scheduling.Our results are promising: (i)On each iteration of distribution estimation,samples obtained with an ILP-assisted DBN have a substantially greater proportion of good solutions than samples generated using a DBN without ILP features, and (ii)On termination of distribution estimation,samples obtained using an ILP-assisted DBN contain more near-optimal samples than samples from a DBN without ILP features.These results suggest that the use of ILP-constructed theories could be useful for incorporating complex domain-knowledge into deep models for estimation of distribution based procedures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge