Comparing Kullback-Leibler Divergence and Mean Squared Error Loss in Knowledge Distillation

Knowledge distillation (KD), transferring knowledge from a cumbersome teacher model to a lightweight student model, has been investigated to design efficient neural architectures. Generally, the objective function of KD is the Kullback-Leibler (KL) divergence loss between the softened probability distributions of the teacher model and the student model with the temperature scaling hyperparameter tau. Despite its widespread use, few studies have discussed the influence of such softening on generalization. Here, we theoretically show that the KL divergence loss focuses on the logit matching when tau increases and the label matching when tau goes to 0 and empirically show that the logit matching is positively correlated to performance improvement in general. From this observation, we consider an intuitive KD loss function, the mean squared error (MSE) between the logit vectors, so that the student model can directly learn the logit of the teacher model. The MSE loss outperforms the KL divergence loss, explained by the difference in the penultimate layer representations between the two losses. Furthermore, we show that sequential distillation can improve performance and that KD, particularly when using the KL divergence loss with small tau, mitigates the label noise. The code to reproduce the experiments is publicly available online at https://github.com/jhoon-oh/kd_data/.

Winning Ticket in Noisy Image Classification

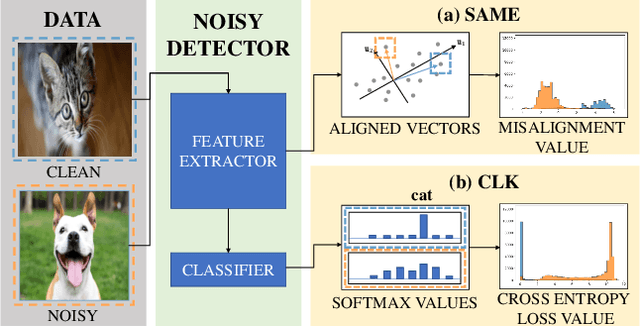
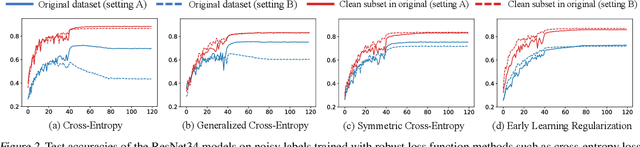
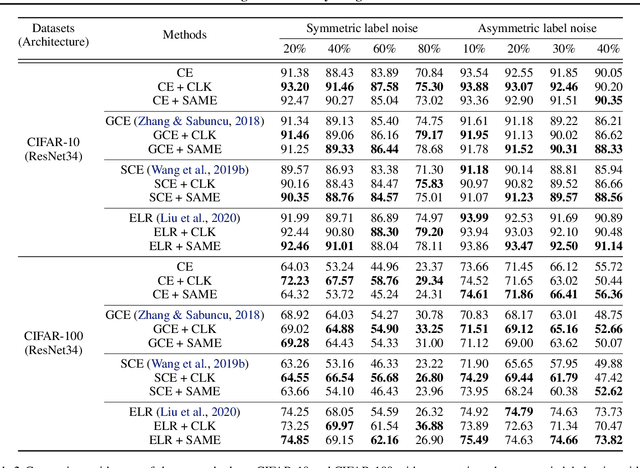
Modern deep neural networks (DNNs) become frail when the datasets contain noisy (incorrect) class labels. Many robust techniques have emerged via loss adjustment, robust loss function, and clean sample selection to mitigate this issue using the whole dataset. Here, we empirically observe that the dataset which contains only clean instances in original noisy datasets leads to better optima than the original dataset even with fewer data. Based on these results, we state the winning ticket hypothesis: regardless of robust methods, any DNNs reach the best performance when trained on the dataset possessing only clean samples from the original (winning ticket). We propose two simple yet effective strategies to identify winning tickets by looking at the loss landscape and latent features in DNNs. We conduct numerical experiments by collaborating the two proposed methods purifying data and existing robust methods for CIFAR-10 and CIFAR-100. The results support that our framework consistently and remarkably improves performance.