Efficient Deep Learning with Decorrelated Backpropagation

The backpropagation algorithm remains the dominant and most successful method for training deep neural networks (DNNs). At the same time, training DNNs at scale comes at a significant computational cost and therefore a high carbon footprint. Converging evidence suggests that input decorrelation may speed up deep learning. However, to date, this has not yet translated into substantial improvements in training efficiency in large-scale DNNs. This is mainly caused by the challenge of enforcing fast and stable network-wide decorrelation. Here, we show for the first time that much more efficient training of very deep neural networks using decorrelated backpropagation is feasible. To achieve this goal we made use of a novel algorithm which induces network-wide input decorrelation using minimal computational overhead. By combining this algorithm with careful optimizations, we obtain a more than two-fold speed-up and higher test accuracy compared to backpropagation when training a 18-layer deep residual network. This demonstrates that decorrelation provides exciting prospects for efficient deep learning at scale.

Effective Learning with Node Perturbation in Deep Neural Networks

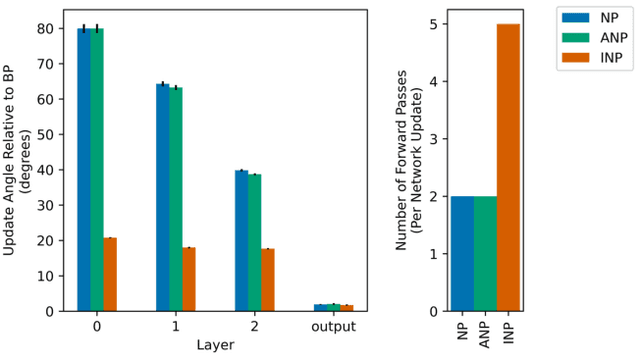
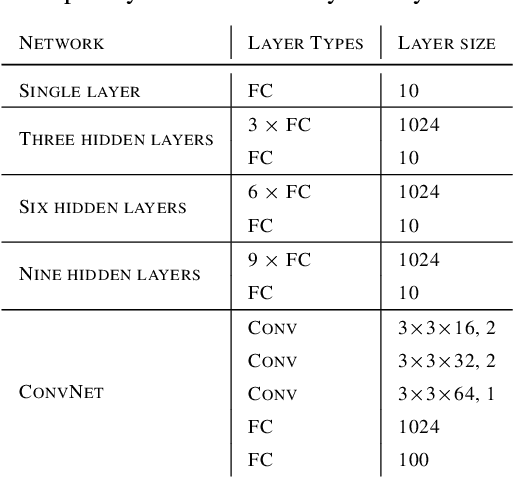
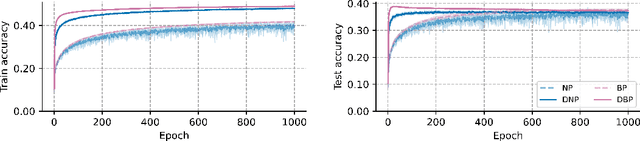
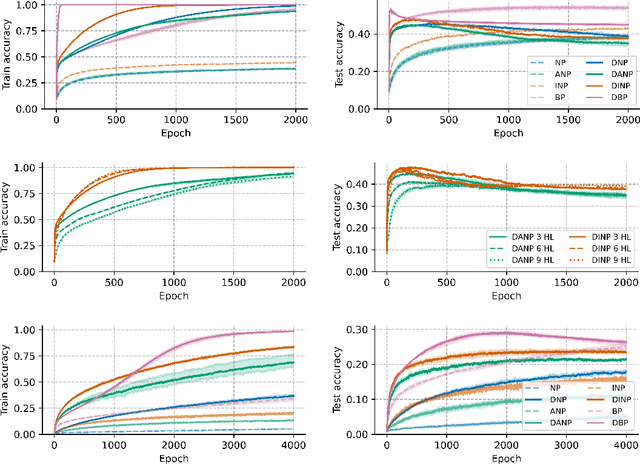
Backpropagation (BP) is the dominant and most successful method for training parameters of deep neural network models. However, BP relies on two computationally distinct phases, does not provide a satisfactory explanation of biological learning, and can be challenging to apply for training of networks with discontinuities or noisy node dynamics. By comparison, node perturbation (NP) proposes learning by the injection of noise into the network activations, and subsequent measurement of the induced loss change. NP relies on two forward (inference) passes, does not make use of network derivatives, and has been proposed as a model for learning in biological systems. However, standard NP is highly data inefficient and unstable due to its unguided, noise-based, activity search. In this work, we investigate different formulations of NP and relate it to the concept of directional derivatives as well as combining it with a decorrelating mechanism for layer-wise inputs. We find that a closer alignment with directional derivatives, and induction of decorrelation of inputs at every layer significantly enhances performance of NP learning making it competitive with BP.

Establishing phone-pair co-usage by comparing mobility patterns

In forensic investigations it is often of value to establish whether two phones were used by the same person during a given time period. We present a method that uses time and location of cell tower registrations of mobile phones to assess the strength of evidence that any pair of phones were used by the same person. The method is transparent as it uses logistic regression to discriminate between the hypotheses of same and different user, and a standard kernel density estimation to quantify the weight of evidence in terms of a likelihood ratio. We further add to previous theoretical work by training and validating our method on real world data, paving the way for application in practice. The method shows good performance under different modeling choices and robustness under lower quantity or quality of data. We discuss practical usage in court.

Scaling up learning with GAIT-prop

Backpropagation of error (BP) is a widely used and highly successful learning algorithm. However, its reliance on non-local information in propagating error gradients makes it seem an unlikely candidate for learning in the brain. In the last decade, a number of investigations have been carried out focused upon determining whether alternative more biologically plausible computations can be used to approximate BP. This work builds on such a local learning algorithm - Gradient Adjusted Incremental Target Propagation (GAIT-prop) - which has recently been shown to approximate BP in a manner which appears biologically plausible. This method constructs local, layer-wise weight update targets in order to enable plausible credit assignment. However, in deep networks, the local weight updates computed by GAIT-prop can deviate from BP for a number of reasons. Here, we provide and test methods to overcome such sources of error. In particular, we adaptively rescale the locally-computed errors and show that this significantly increases the performance and stability of the GAIT-prop algorithm when applied to the CIFAR-10 dataset.