Effective Learning with Node Perturbation in Deep Neural Networks

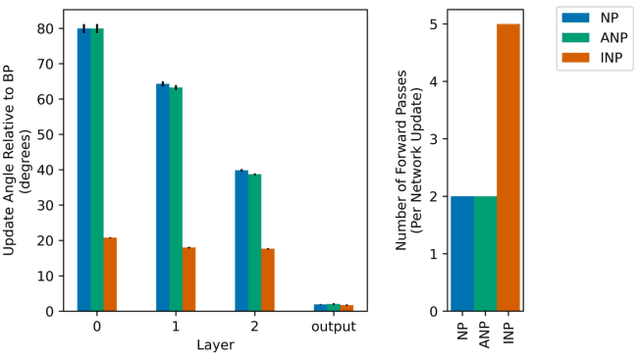
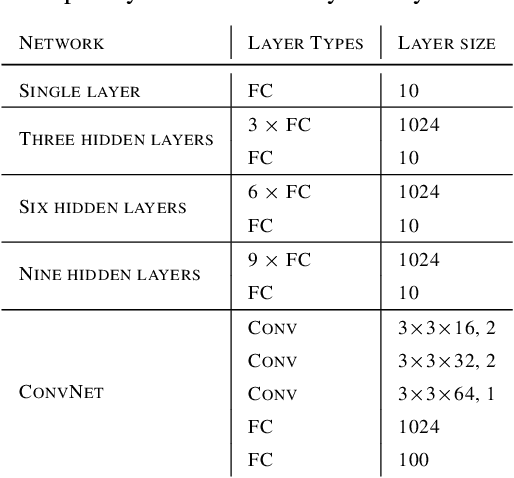
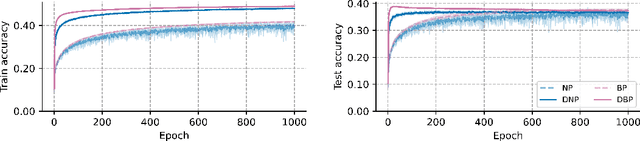
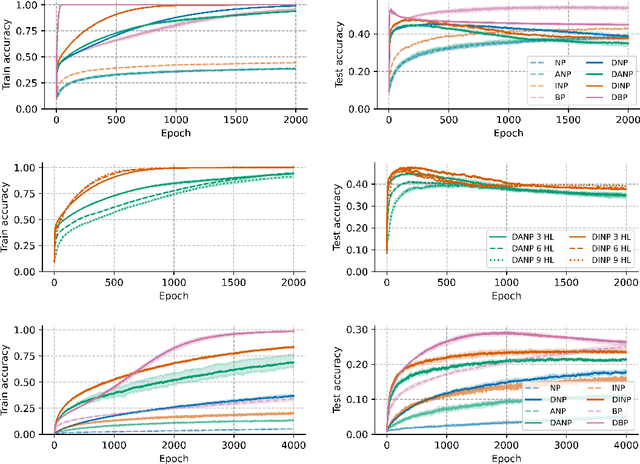
Backpropagation (BP) is the dominant and most successful method for training parameters of deep neural network models. However, BP relies on two computationally distinct phases, does not provide a satisfactory explanation of biological learning, and can be challenging to apply for training of networks with discontinuities or noisy node dynamics. By comparison, node perturbation (NP) proposes learning by the injection of noise into the network activations, and subsequent measurement of the induced loss change. NP relies on two forward (inference) passes, does not make use of network derivatives, and has been proposed as a model for learning in biological systems. However, standard NP is highly data inefficient and unstable due to its unguided, noise-based, activity search. In this work, we investigate different formulations of NP and relate it to the concept of directional derivatives as well as combining it with a decorrelating mechanism for layer-wise inputs. We find that a closer alignment with directional derivatives, and induction of decorrelation of inputs at every layer significantly enhances performance of NP learning making it competitive with BP.