Local Intrinsic Dimensionality Signals Adversarial Perturbations

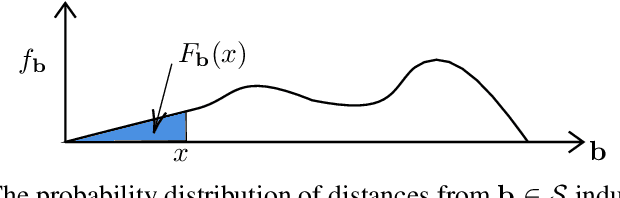
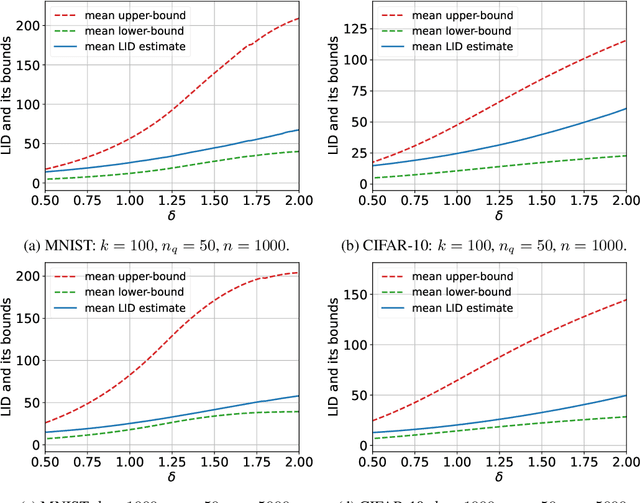
The vulnerability of machine learning models to adversarial perturbations has motivated a significant amount of research under the broad umbrella of adversarial machine learning. Sophisticated attacks may cause learning algorithms to learn decision functions or make decisions with poor predictive performance. In this context, there is a growing body of literature that uses local intrinsic dimensionality (LID), a local metric that describes the minimum number of latent variables required to describe each data point, for detecting adversarial samples and subsequently mitigating their effects. The research to date has tended to focus on using LID as a practical defence method often without fully explaining why LID can detect adversarial samples. In this paper, we derive a lower-bound and an upper-bound for the LID value of a perturbed data point and demonstrate that the bounds, in particular the lower-bound, has a positive correlation with the magnitude of the perturbation. Hence, we demonstrate that data points that are perturbed by a large amount would have large LID values compared to unperturbed samples, thus justifying its use in the prior literature. Furthermore, our empirical validation demonstrates the validity of the bounds on benchmark datasets.

Defending Distributed Classifiers Against Data Poisoning Attacks

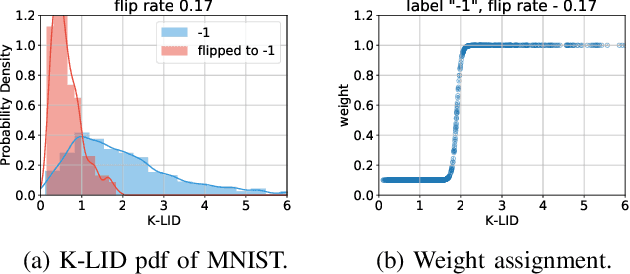
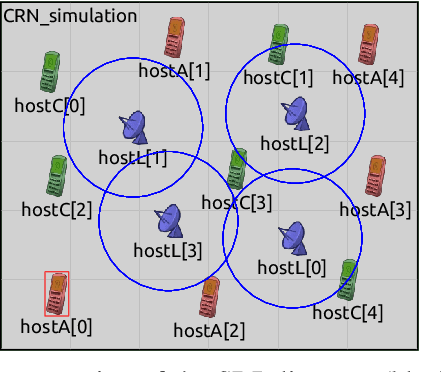
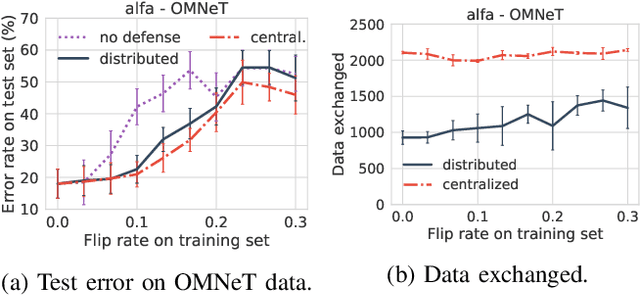
Support Vector Machines (SVMs) are vulnerable to targeted training data manipulations such as poisoning attacks and label flips. By carefully manipulating a subset of training samples, the attacker forces the learner to compute an incorrect decision boundary, thereby cause misclassifications. Considering the increased importance of SVMs in engineering and life-critical applications, we develop a novel defense algorithm that improves resistance against such attacks. Local Intrinsic Dimensionality (LID) is a promising metric that characterizes the outlierness of data samples. In this work, we introduce a new approximation of LID called K-LID that uses kernel distance in the LID calculation, which allows LID to be calculated in high dimensional transformed spaces. We introduce a weighted SVM against such attacks using K-LID as a distinguishing characteristic that de-emphasizes the effect of suspicious data samples on the SVM decision boundary. Each sample is weighted on how likely its K-LID value is from the benign K-LID distribution rather than the attacked K-LID distribution. We then demonstrate how the proposed defense can be applied to a distributed SVM framework through a case study on an SDR-based surveillance system. Experiments with benchmark data sets show that the proposed defense reduces classification error rates substantially (10% on average).

Defending Regression Learners Against Poisoning Attacks

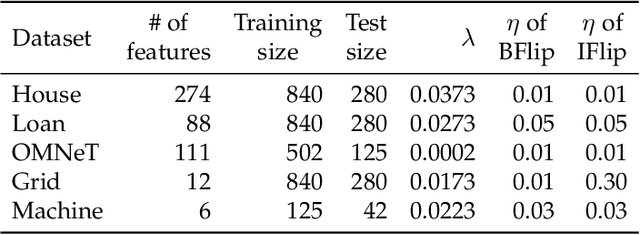
Regression models, which are widely used from engineering applications to financial forecasting, are vulnerable to targeted malicious attacks such as training data poisoning, through which adversaries can manipulate their predictions. Previous works that attempt to address this problem rely on assumptions about the nature of the attack/attacker or overestimate the knowledge of the learner, making them impractical. We introduce a novel Local Intrinsic Dimensionality (LID) based measure called N-LID that measures the local deviation of a given data point's LID with respect to its neighbors. We then show that N-LID can distinguish poisoned samples from normal samples and propose an N-LID based defense approach that makes no assumptions of the attacker. Through extensive numerical experiments with benchmark datasets, we show that the proposed defense mechanism outperforms the state of the art defenses in terms of prediction accuracy (up to 76% lower MSE compared to an undefended ridge model) and running time.