Local Intrinsic Dimensionality Signals Adversarial Perturbations
Paper and Code
Sep 24, 2021

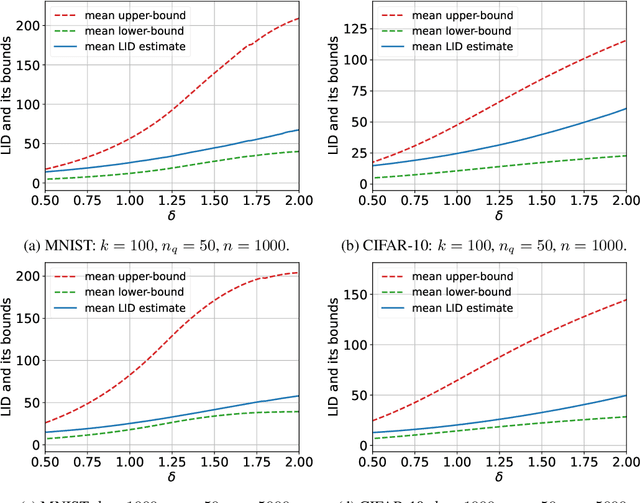
The vulnerability of machine learning models to adversarial perturbations has motivated a significant amount of research under the broad umbrella of adversarial machine learning. Sophisticated attacks may cause learning algorithms to learn decision functions or make decisions with poor predictive performance. In this context, there is a growing body of literature that uses local intrinsic dimensionality (LID), a local metric that describes the minimum number of latent variables required to describe each data point, for detecting adversarial samples and subsequently mitigating their effects. The research to date has tended to focus on using LID as a practical defence method often without fully explaining why LID can detect adversarial samples. In this paper, we derive a lower-bound and an upper-bound for the LID value of a perturbed data point and demonstrate that the bounds, in particular the lower-bound, has a positive correlation with the magnitude of the perturbation. Hence, we demonstrate that data points that are perturbed by a large amount would have large LID values compared to unperturbed samples, thus justifying its use in the prior literature. Furthermore, our empirical validation demonstrates the validity of the bounds on benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge