Unrolled Optimization with Deep Learning-based Priors for Phaseless Inverse Scattering Problems

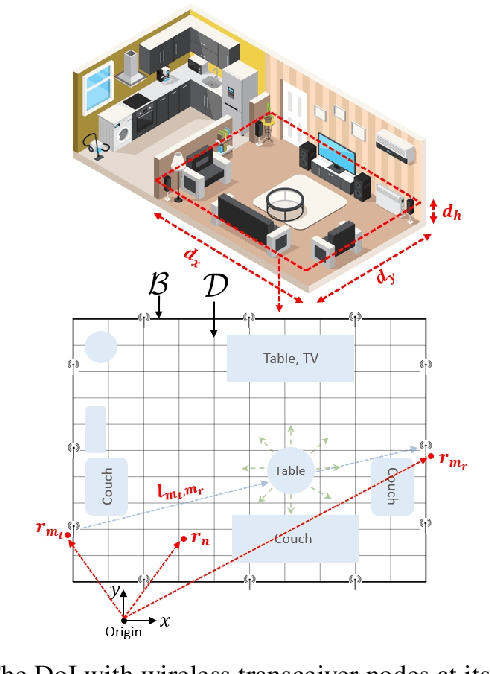
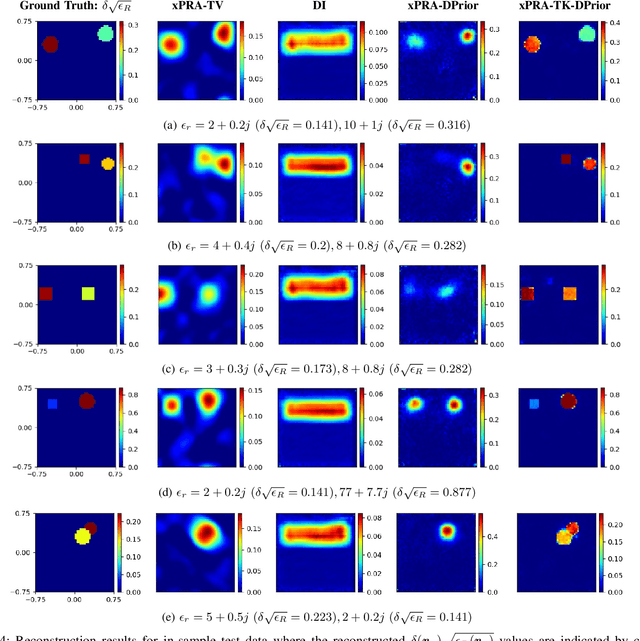
Inverse scattering problems, such as those in electromagnetic imaging using phaseless data (PD-ISPs), involve imaging objects using phaseless measurements of wave scattering. Such inverse problems can be highly non-linear and ill-posed under extremely strong scattering conditions such as when the objects have very high permittivity or are large in size. In this work, we propose an end-to-end reconstruction framework using unrolled optimization with deep priors to solve PD-ISPs under very strong scattering conditions. We incorporate an approximate linear physics-based model into our optimization framework along with a deep learning-based prior and solve the resulting problem using an iterative algorithm which is unfolded into a deep network. This network not only learns data-driven regularization, but also overcomes the shortcomings of approximate linear models and learns non-linear features. More important, unlike existing PD-ISP methods, the proposed framework learns optimum values of all tunable parameters (including multiple regularization parameters) as a part of the framework. Results from simulations and experiments are shown for the use case of indoor imaging using 2.4 GHz phaseless Wi-Fi measurements, where the objects exhibit extremely strong scattering and low-absorption. Results show that the proposed framework outperforms existing model-driven and data-driven techniques by a significant margin and provides up to 20 times higher validity range.

Physics Assisted Deep Learning for Indoor Imaging using Phaseless Wi-Fi Measurements

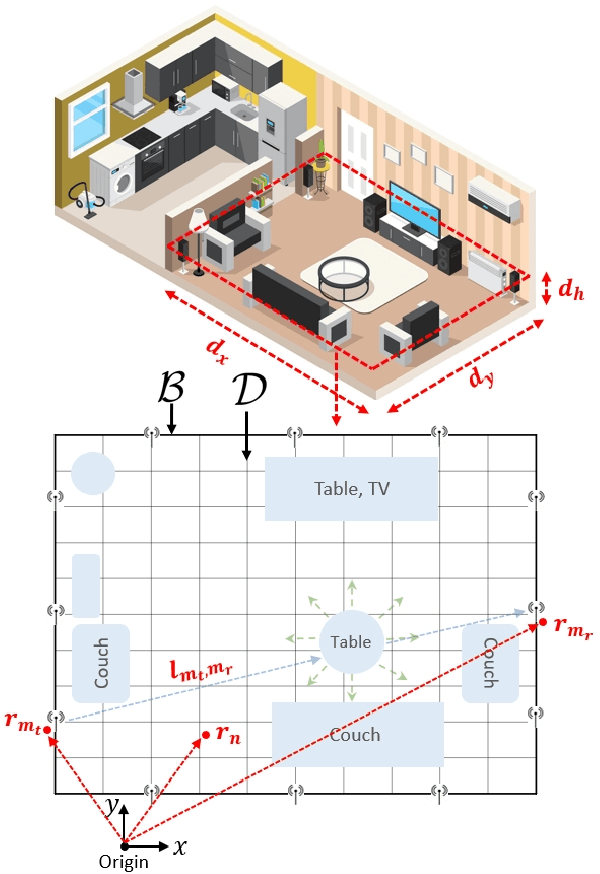
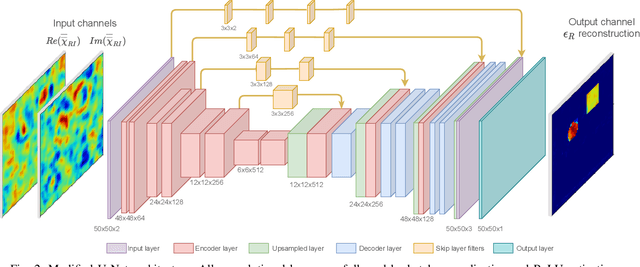
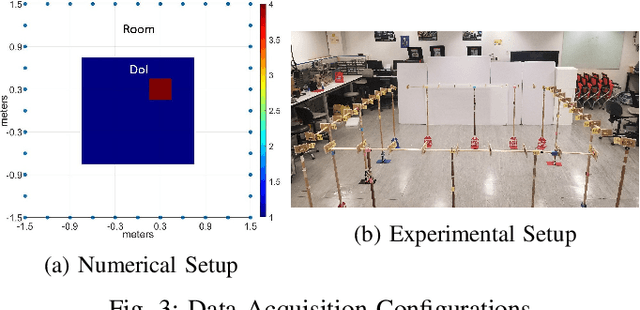
A physics assisted deep learning framework to perform accurate indoor imaging using phaseless Wi-Fi measurements is proposed. It is able to image objects that are large (compared to wavelength) and have high permittivity values, that existing radio frequency (RF) inverse scattering techniques find very challenging, making it suitable for indoor RF imaging. The technique utilizes a Rytov based inverse scattering model with a deep learning framework. The inverse scattering model is based on an extended Rytov approximation (xRA) that pre-reconstructs the RF measurements. Under strong scattering conditions, this pre-reconstruction is related to the actual permittivity profile by a non-linear function, which is learned by a modified U-Net model to obtain the permittivity profile of the object. Thus, our proposed approach not only reconstructs the shape of objects, but also estimates their permittivity values accurately. We demonstrate its imaging performance using simulations as well as experimental results in an actual indoor environment using 2.4 GHz Wi-Fi phaseless measurements. For incident wavelength $\lambda_0$, the proposed framework can reconstruct objects with relative permittivity as high as 77 and electrical size as large as $40 \lambda$, where $\lambda =\lambda_0/\sqrt{77}$. This is in contrast to existing phaseless imaging techniques which cannot reconstruct permittivity values beyond 3 or 4. Thus, our proposed method is the first inverse scattering-based deep learning framework which can image large scatterers with high permittivity and achieve accurate indoor RF imaging using phaseless Wi-Fi measurements.

Accurate Indoor Radio Frequency Imaging using a New Extended Rytov Approximation for Lossy Media

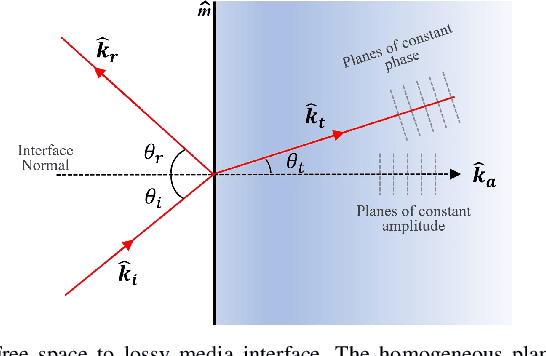
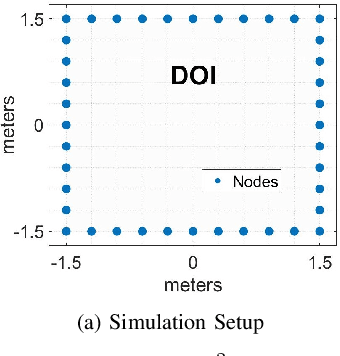
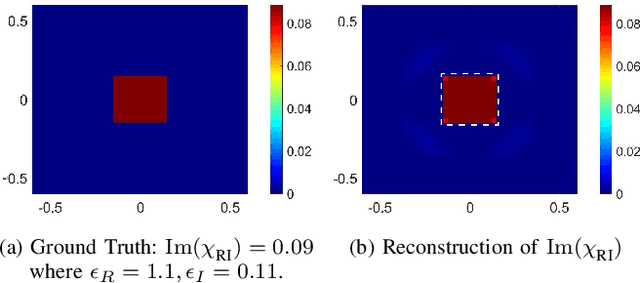
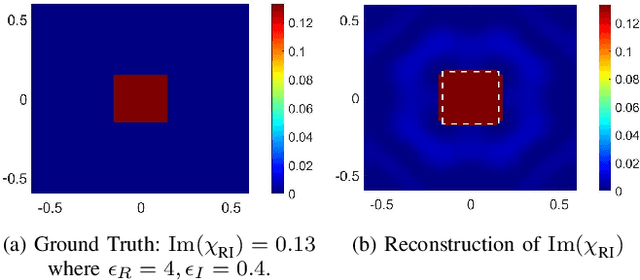
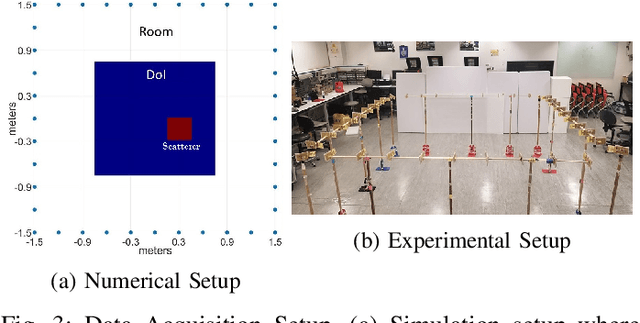
Imaging objects with high relative permittivity and large electrical size remains a challenging problem in the field of inverse scattering. In this work we present a phaseless inverse scattering method that can accurately image and reconstruct objects even with these attributes. The reconstruction accuracy obtained under these conditions has not been achieved previously and can therefore open up the area to technologically important applications such as indoor Radio Frequency (RF) and microwave imaging. The novelty of the approach is that it utilizes a high frequency approximation for waves passing through lossy media to provide corrections to the conventional Rytov approximation (RA). We refer to this technique as the Extended Phaseless Rytov Approximation for Low Loss Media (xPRA-LM). Simulation as well as experimental results are provided for indoor RF imaging using phaseless measurements from 2.4 GHz based WiFi nodes. We demonstrate that the approach provides accurate reconstruction of an object up to relative permittivities of $15+j1.5$ for object sizes greater than $20 \lambda$ ($\lambda$ is wavelength inside object). Even at higher relative permittivities of up to $\epsilon_r=77+j 7$, object shape reconstruction remains accurate, however the reconstruction amplitude is less accurate. These results have not been obtained before and can be utilized to achieve the potential of RF and microwave imaging in applications such as indoor RF imaging.

Improved Covariance Matrix Estimator using Shrinkage Transformation and Random Matrix Theory

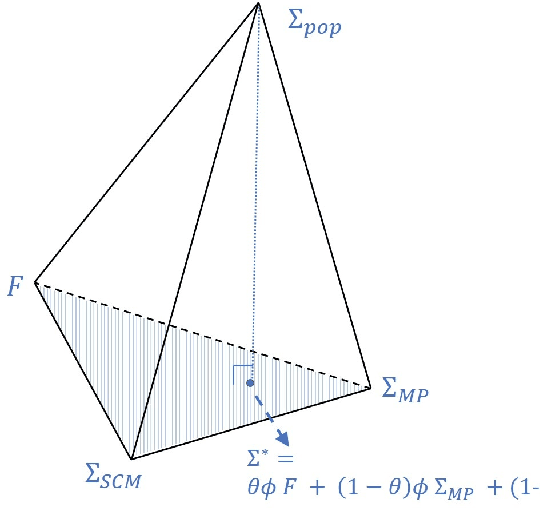
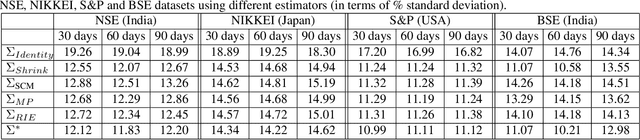
One of the major challenges in multivariate analysis is the estimation of population covariance matrix from sample covariance matrix (SCM). Most recent covariance matrix estimators use either shrinkage transformations or asymptotic results from Random Matrix Theory (RMT). Shrinkage techniques help in pulling extreme correlation values towards certain target values whereas tools from RMT help in removing noisy eigenvalues of SCM. Both of these techniques use different approaches to achieve a similar goal which is to remove noisy correlations and add structure to SCM to overcome the bias-variance trade-off. In this paper, we first critically evaluate the pros and cons of these two techniques and then propose an improved estimator which exploits the advantages of both by taking an optimally weighted convex combination of covariance matrices estimated by an improved shrinkage transformation and a RMT based filter. It is a generalized estimator which can adapt to changing sampling noise conditions in various datasets by performing hyperparameter optimization. We show the effectiveness of this estimator on the problem of designing a financial portfolio with minimum risk. We have chosen this problem because the complex properties of stock market data provide extreme conditions to test the robustness of a covariance estimator. Using data from four of the world's largest stock exchanges, we show that our proposed estimator outperforms existing estimators in minimizing the out-of-sample risk of the portfolio and hence predicts population statistics more precisely. Since covariance analysis is a crucial statistical tool, this estimator can be used in a wide range of machine learning, signal processing and high dimensional pattern recognition applications.