Improved Covariance Matrix Estimator using Shrinkage Transformation and Random Matrix Theory

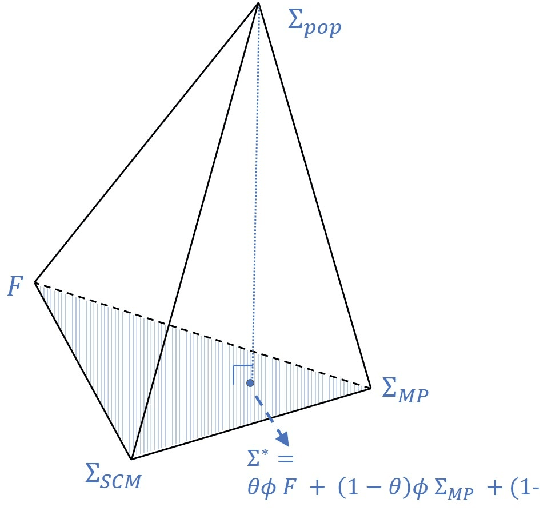
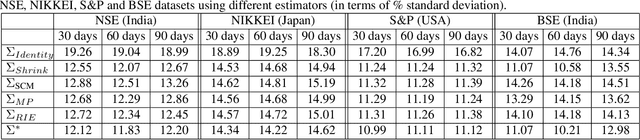
One of the major challenges in multivariate analysis is the estimation of population covariance matrix from sample covariance matrix (SCM). Most recent covariance matrix estimators use either shrinkage transformations or asymptotic results from Random Matrix Theory (RMT). Shrinkage techniques help in pulling extreme correlation values towards certain target values whereas tools from RMT help in removing noisy eigenvalues of SCM. Both of these techniques use different approaches to achieve a similar goal which is to remove noisy correlations and add structure to SCM to overcome the bias-variance trade-off. In this paper, we first critically evaluate the pros and cons of these two techniques and then propose an improved estimator which exploits the advantages of both by taking an optimally weighted convex combination of covariance matrices estimated by an improved shrinkage transformation and a RMT based filter. It is a generalized estimator which can adapt to changing sampling noise conditions in various datasets by performing hyperparameter optimization. We show the effectiveness of this estimator on the problem of designing a financial portfolio with minimum risk. We have chosen this problem because the complex properties of stock market data provide extreme conditions to test the robustness of a covariance estimator. Using data from four of the world's largest stock exchanges, we show that our proposed estimator outperforms existing estimators in minimizing the out-of-sample risk of the portfolio and hence predicts population statistics more precisely. Since covariance analysis is a crucial statistical tool, this estimator can be used in a wide range of machine learning, signal processing and high dimensional pattern recognition applications.