Ensuring Reliable Robot Task Performance through Probabilistic Rare-Event Verification and Synthesis

Providing guarantees on the safe operation of robots against edge cases is challenging as testing methods such as traditional Monte-Carlo require too many samples to provide reasonable statistics. Built upon recent advancements in rare-event sampling, we present a model-based method to verify if a robotic system satisfies a Signal Temporal Logic (STL) specification in the face of environment variations and sensor/actuator noises. Our method is efficient and applicable to both linear and nonlinear and even black-box systems with arbitrary, but known, uncertainty distributions. For linear systems with Gaussian uncertainties, we exploit a feature to find optimal parameters that minimize the probability of failure. We demonstrate illustrative examples on applying our approach to real-world autonomous robotic systems.

Elliptical Slice Sampling for Probabilistic Verification of Stochastic Systems with Signal Temporal Logic Specifications

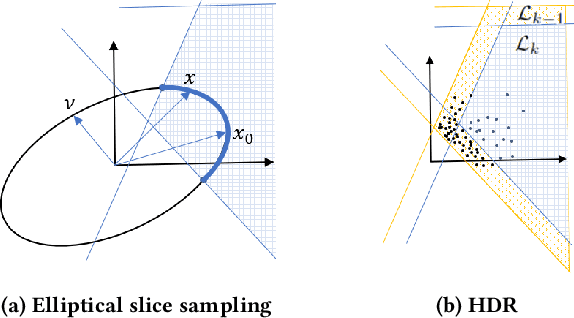
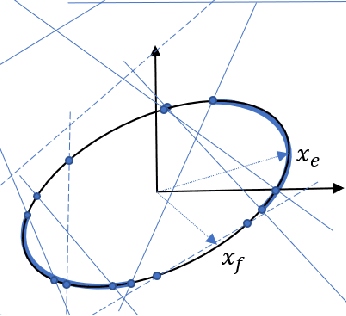
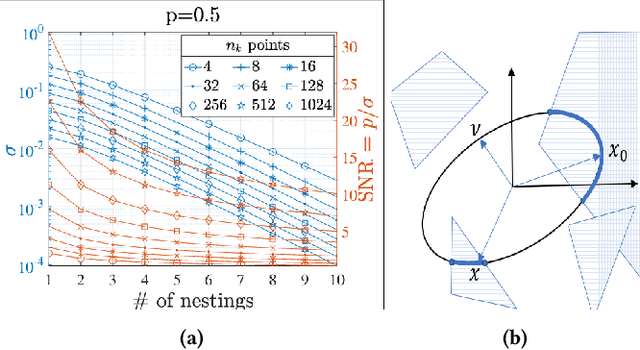
Autonomous robots typically incorporate complex sensors in their decision-making and control loops. These sensors, such as cameras and Lidars, have imperfections in their sensing and are influenced by environmental conditions. In this paper, we present a method for probabilistic verification of linearizable systems with Gaussian and Gaussian mixture noise models (e.g. from perception modules, machine learning components). We compute the probabilities of task satisfaction under Signal Temporal Logic (STL) specifications, using its robustness semantics, with a Markov Chain Monte-Carlo slice sampler. As opposed to other techniques, our method avoids over-approximations and double-counting of failure events. Central to our approach is a method for efficient and rejection-free sampling of signals from a Gaussian distribution such that satisfy or violate a given STL formula. We show illustrative examples from applications in robot motion planning.

Sampling-based Polytopic Trees for Approximate Optimal Control of Piecewise Affine Systems

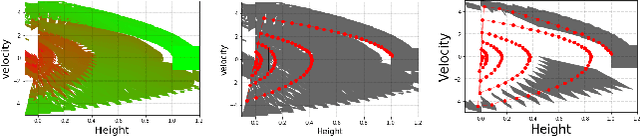
Piecewise affine (PWA) systems are widely used to model highly nonlinear behaviors such as contact dynamics in robot locomotion and manipulation. Existing control techniques for PWA systems have computational drawbacks, both in offline design and online implementation. In this paper, we introduce a method to obtain feedback control policies and a corresponding set of admissible initial conditions for discrete-time PWA systems such that all the closed-loop trajectories reach a goal polytope, while a cost function is optimized. The idea is conceptually similar to LQR-trees \cite{tedrake2010lqr}, which consists of 3 steps: (1) open-loop trajectory optimization, (2) feedback control for computation of "funnels" of states around trajectories, and (3) repeating (1) and (2) in a way that the funnels are grown backward from the goal in a tree fashion and fill the state-space as much as possible. We show PWA dynamics can be exploited to combine step (1) and (2) into a single step that is tackled using mixed-integer convex programming, which makes the method suitable for dealing with hard constraints. Illustrative examples on contact-based dynamics are presented.

Robotic Swarm Control from Spatio-Temporal Specifications

In this paper, we study the problem of controlling a two-dimensional robotic swarm with the purpose of achieving high level and complex spatio-temporal patterns. We use a rich spatio-temporal logic that is capable of describing a wide range of time varying and complex spatial configurations, and develop a method to encode such formal specifications as a set of mixed integer linear constraints, which are incorporated into a mixed integer linear programming problem. We plan trajectories for each individual robot such that the whole swarm satisfies the spatio-temporal requirements, while optimizing total robot movement and/or a metric that shows how strongly the swarm trajectory resembles given spatio-temporal behaviors. An illustrative case study is included.