Sampling-based Polytopic Trees for Approximate Optimal Control of Piecewise Affine Systems
Paper and Code
Sep 25, 2018

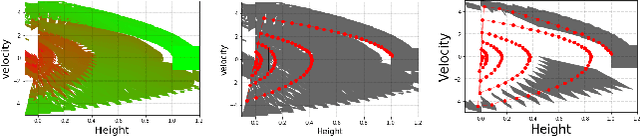

Piecewise affine (PWA) systems are widely used to model highly nonlinear behaviors such as contact dynamics in robot locomotion and manipulation. Existing control techniques for PWA systems have computational drawbacks, both in offline design and online implementation. In this paper, we introduce a method to obtain feedback control policies and a corresponding set of admissible initial conditions for discrete-time PWA systems such that all the closed-loop trajectories reach a goal polytope, while a cost function is optimized. The idea is conceptually similar to LQR-trees \cite{tedrake2010lqr}, which consists of 3 steps: (1) open-loop trajectory optimization, (2) feedback control for computation of "funnels" of states around trajectories, and (3) repeating (1) and (2) in a way that the funnels are grown backward from the goal in a tree fashion and fill the state-space as much as possible. We show PWA dynamics can be exploited to combine step (1) and (2) into a single step that is tackled using mixed-integer convex programming, which makes the method suitable for dealing with hard constraints. Illustrative examples on contact-based dynamics are presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge