Elliptical Slice Sampling for Probabilistic Verification of Stochastic Systems with Signal Temporal Logic Specifications
Paper and Code
Feb 28, 2022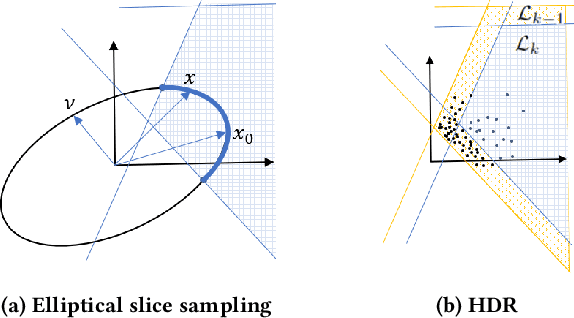
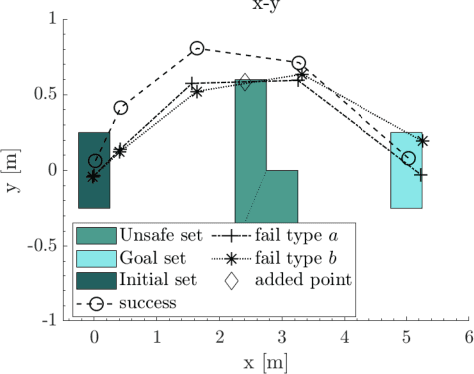
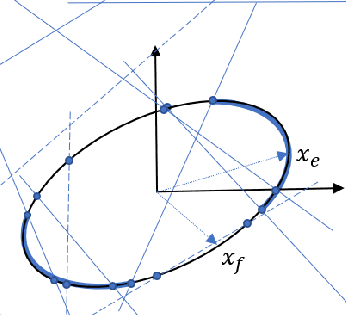
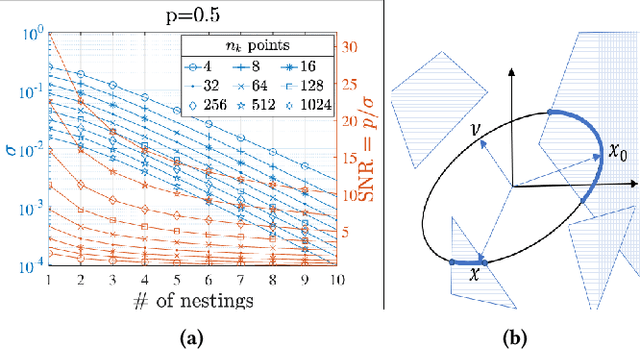
Autonomous robots typically incorporate complex sensors in their decision-making and control loops. These sensors, such as cameras and Lidars, have imperfections in their sensing and are influenced by environmental conditions. In this paper, we present a method for probabilistic verification of linearizable systems with Gaussian and Gaussian mixture noise models (e.g. from perception modules, machine learning components). We compute the probabilities of task satisfaction under Signal Temporal Logic (STL) specifications, using its robustness semantics, with a Markov Chain Monte-Carlo slice sampler. As opposed to other techniques, our method avoids over-approximations and double-counting of failure events. Central to our approach is a method for efficient and rejection-free sampling of signals from a Gaussian distribution such that satisfy or violate a given STL formula. We show illustrative examples from applications in robot motion planning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge