In-Materia Speech Recognition

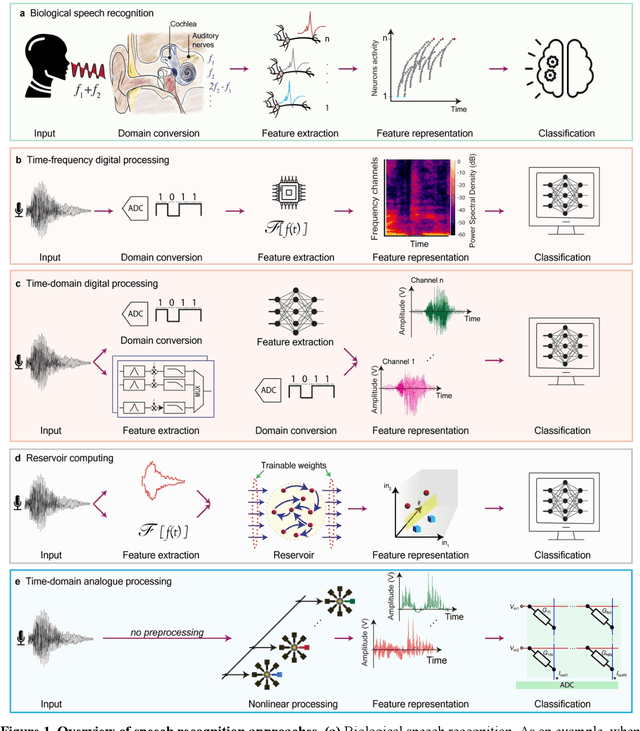
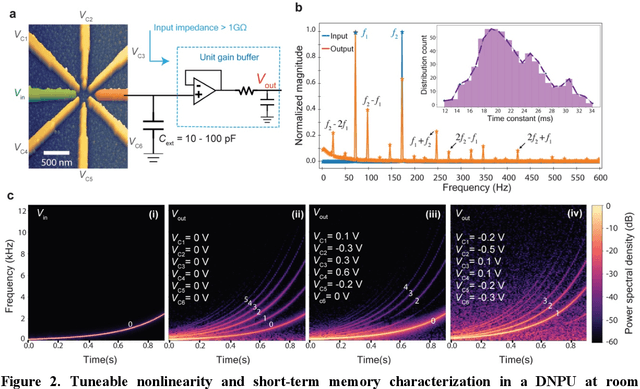
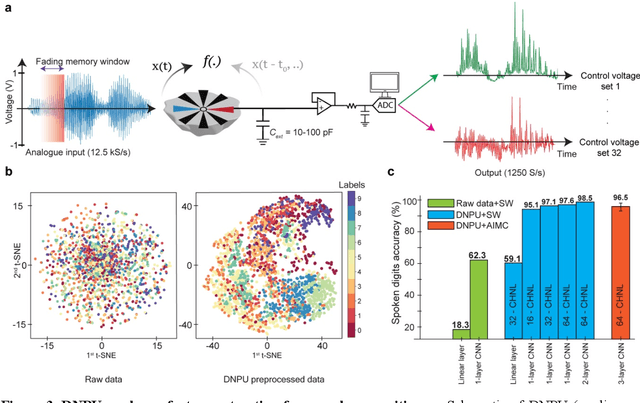
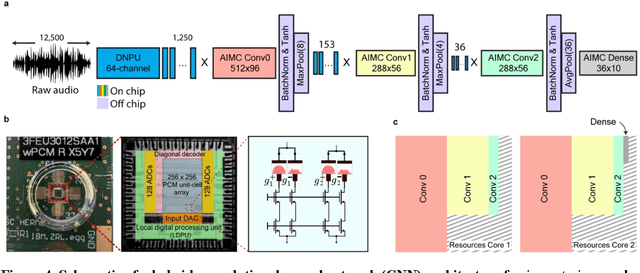
With the rise of decentralized computing, as in the Internet of Things, autonomous driving, and personalized healthcare, it is increasingly important to process time-dependent signals at the edge efficiently: right at the place where the temporal data are collected, avoiding time-consuming, insecure, and costly communication with a centralized computing facility (or cloud). However, modern-day processors often cannot meet the restrained power and time budgets of edge systems because of intrinsic limitations imposed by their architecture (von Neumann bottleneck) or domain conversions (analogue-to-digital and time-to-frequency). Here, we propose an edge temporal-signal processor based on two in-materia computing systems for both feature extraction and classification, reaching a software-level accuracy of 96.2% for the TI-46-Word speech-recognition task. First, a nonlinear, room-temperature dopant-network-processing-unit (DNPU) layer realizes analogue, time-domain feature extraction from the raw audio signals, similar to the human cochlea. Second, an analogue in-memory computing (AIMC) chip, consisting of memristive crossbar arrays, implements a compact neural network trained on the extracted features for classification. With the DNPU feature extraction consuming 100s nW and AIMC-based classification having the potential for less than 10 fJ per multiply-accumulate operation, our findings offer a promising avenue for advancing the compactness, efficiency, and performance of heterogeneous smart edge processors through in-materia computing hardware.

A Quantum Computing Approach for Multi-robot Coverage Path Planning

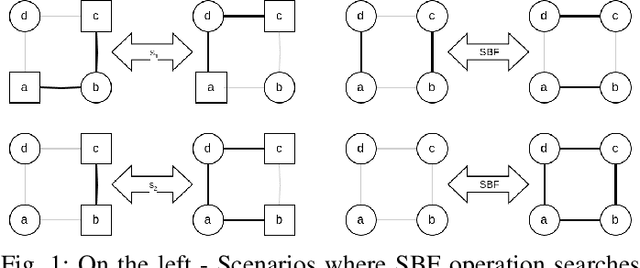
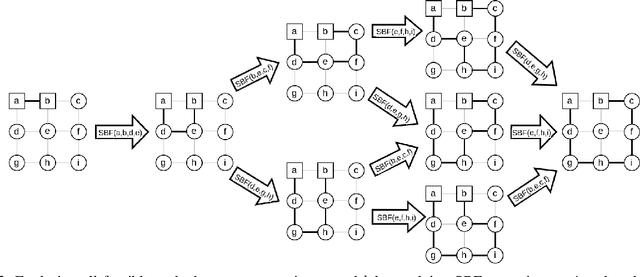
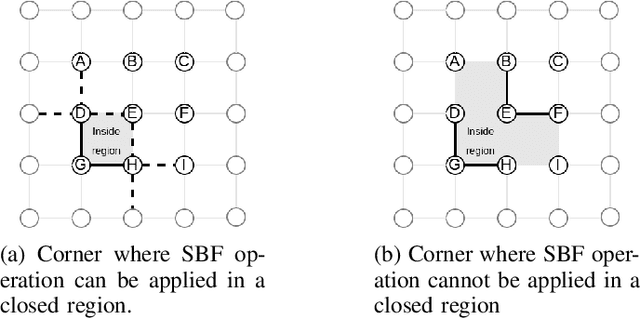
This paper tackles the multi-vehicle Coverage Path Planning (CPP) problem, crucial for applications like search and rescue or environmental monitoring. Due to its NP-hard nature, finding optimal solutions becomes infeasible with larger problem sizes. This motivates the development of heuristic approaches that enhance efficiency even marginally. We propose a novel approach for exploring paths in a 2D grid, specifically designed for easy integration with the Quantum Alternating Operator Ansatz (QAOA), a powerful quantum heuristic. Our contribution includes: 1) An objective function tailored to solve the multi-vehicle CPP using QAOA. 2) Theoretical proofs guaranteeing the validity of the proposed approach. 3) Efficient construction of QAOA operators for practical implementation. 4) Resource estimation to assess the feasibility of QAOA execution. 5) Performance comparison against established algorithms like the Depth First Search. This work paves the way for leveraging quantum computing in optimizing multi-vehicle path planning, potentially leading to real-world advancements in various applications.