Probabilistic PARAFAC2

The PARAFAC2 is a multimodal factor analysis model suitable for analyzing multi-way data when one of the modes has incomparable observation units, for example because of differences in signal sampling or batch sizes. A fully probabilistic treatment of the PARAFAC2 is desirable in order to improve robustness to noise and provide a well founded principle for determining the number of factors, but challenging because the factor loadings are constrained to be orthogonal. We develop two probabilistic formulations of the PARAFAC2 along with variational procedures for inference: In the one approach, the mean values of the factor loadings are orthogonal leading to closed form variational updates, and in the other, the factor loadings themselves are orthogonal using a matrix Von Mises-Fisher distribution. We contrast our probabilistic formulation to the conventional direct fitting algorithm based on maximum likelihood. On simulated data and real fluorescence spectroscopy and gas chromatography-mass spectrometry data, we compare our approach to the conventional PARAFAC2 model estimation and find that the probabilistic formulation is more robust to noise and model order misspecification. The probabilistic PARAFAC2 thus forms a promising framework for modeling multi-way data accounting for uncertainty.

Scalable Group Level Probabilistic Sparse Factor Analysis

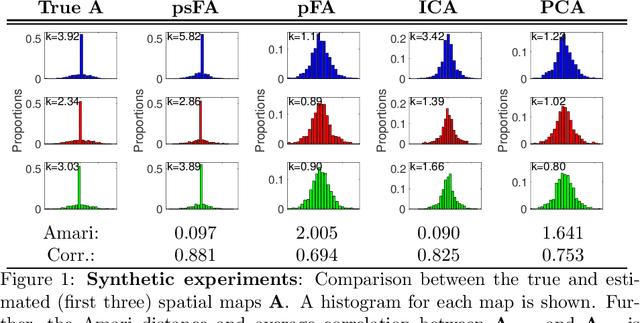
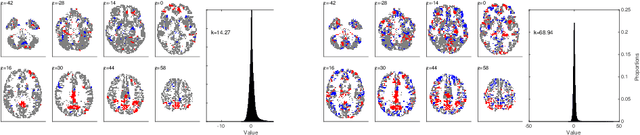
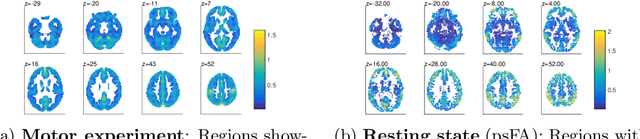
Many data-driven approaches exist to extract neural representations of functional magnetic resonance imaging (fMRI) data, but most of them lack a proper probabilistic formulation. We propose a group level scalable probabilistic sparse factor analysis (psFA) allowing spatially sparse maps, component pruning using automatic relevance determination (ARD) and subject specific heteroscedastic spatial noise modeling. For task-based and resting state fMRI, we show that the sparsity constraint gives rise to components similar to those obtained by group independent component analysis. The noise modeling shows that noise is reduced in areas typically associated with activation by the experimental design. The psFA model identifies sparse components and the probabilistic setting provides a natural way to handle parameter uncertainties. The variational Bayesian framework easily extends to more complex noise models than the presently considered.

Nonparametric Modeling of Dynamic Functional Connectivity in fMRI Data

Dynamic functional connectivity (FC) has in recent years become a topic of interest in the neuroimaging community. Several models and methods exist for both functional magnetic resonance imaging (fMRI) and electroencephalography (EEG), and the results point towards the conclusion that FC exhibits dynamic changes. The existing approaches modeling dynamic connectivity have primarily been based on time-windowing the data and k-means clustering. We propose a non-parametric generative model for dynamic FC in fMRI that does not rely on specifying window lengths and number of dynamic states. Rooted in Bayesian statistical modeling we use the predictive likelihood to investigate if the model can discriminate between a motor task and rest both within and across subjects. We further investigate what drives dynamic states using the model on the entire data collated across subjects and task/rest. We find that the number of states extracted are driven by subject variability and preprocessing differences while the individual states are almost purely defined by either task or rest. This questions how we in general interpret dynamic FC and points to the need for more research on what drives dynamic FC.