Probabilistic PARAFAC2

The PARAFAC2 is a multimodal factor analysis model suitable for analyzing multi-way data when one of the modes has incomparable observation units, for example because of differences in signal sampling or batch sizes. A fully probabilistic treatment of the PARAFAC2 is desirable in order to improve robustness to noise and provide a well founded principle for determining the number of factors, but challenging because the factor loadings are constrained to be orthogonal. We develop two probabilistic formulations of the PARAFAC2 along with variational procedures for inference: In the one approach, the mean values of the factor loadings are orthogonal leading to closed form variational updates, and in the other, the factor loadings themselves are orthogonal using a matrix Von Mises-Fisher distribution. We contrast our probabilistic formulation to the conventional direct fitting algorithm based on maximum likelihood. On simulated data and real fluorescence spectroscopy and gas chromatography-mass spectrometry data, we compare our approach to the conventional PARAFAC2 model estimation and find that the probabilistic formulation is more robust to noise and model order misspecification. The probabilistic PARAFAC2 thus forms a promising framework for modeling multi-way data accounting for uncertainty.

Scalable Group Level Probabilistic Sparse Factor Analysis

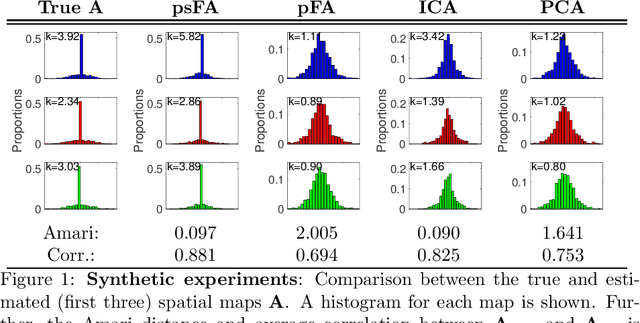
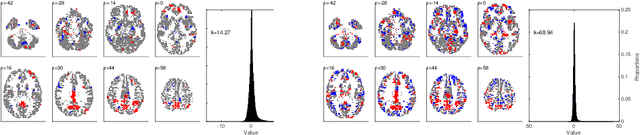
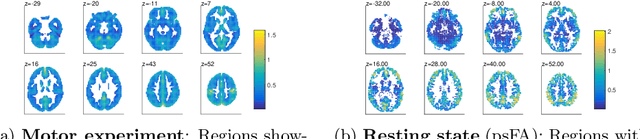
Many data-driven approaches exist to extract neural representations of functional magnetic resonance imaging (fMRI) data, but most of them lack a proper probabilistic formulation. We propose a group level scalable probabilistic sparse factor analysis (psFA) allowing spatially sparse maps, component pruning using automatic relevance determination (ARD) and subject specific heteroscedastic spatial noise modeling. For task-based and resting state fMRI, we show that the sparsity constraint gives rise to components similar to those obtained by group independent component analysis. The noise modeling shows that noise is reduced in areas typically associated with activation by the experimental design. The psFA model identifies sparse components and the probabilistic setting provides a natural way to handle parameter uncertainties. The variational Bayesian framework easily extends to more complex noise models than the presently considered.