Nicolai A. B. Riis
Structural Gaussian Priors for Bayesian CT reconstruction of Subsea Pipes
Mar 02, 2022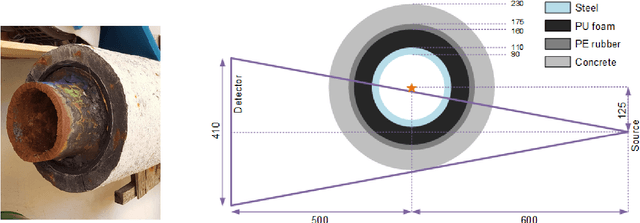
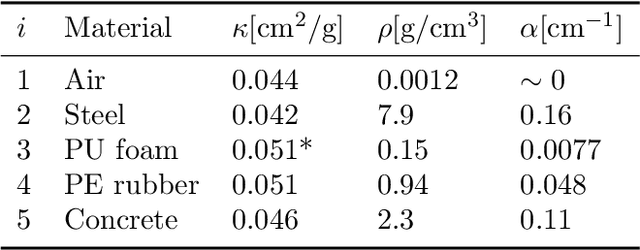
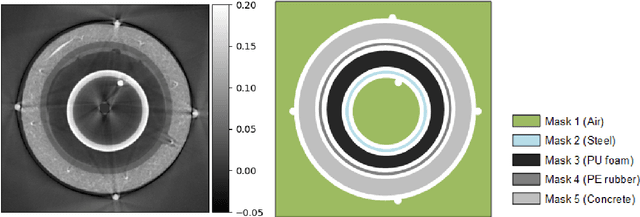
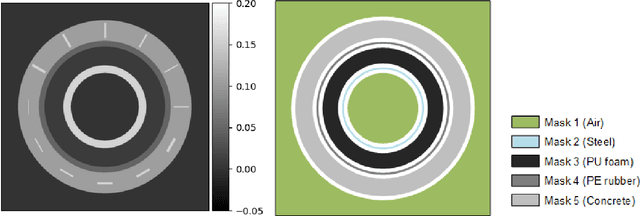
Abstract:A non-destructive testing (NDT) application of X-ray computed tomography (CT) is inspection of subsea pipes in operation via 2D cross-sectional scans. Data acquisition is time-consuming and costly due to the challenging subsea environment. Reducing the number of projections in a scan can yield time and cost savings, but compromises the reconstruction quality, if conventional reconstruction methods are used. In this work we take a Bayesian approach to CT reconstruction and focus on designing an effective prior to make use of available structural information about the pipe geometry. We propose a new class of structural Gaussian priors to enforce expected material properties in different regions of the reconstructed image based on independent Gaussian priors in combination with global regularity through a Gaussian Markov Random Field (GMRF) prior. Numerical experiments with synthetic and real data show that the proposed structural Gaussian prior can reduce artifacts and enhance contrast in the reconstruction compared to using only a global GMRF prior or no prior at all. We show how the resulting posterior distribution can be efficiently sampled even for large-scale images, which is essential for practical NDT applications.
Scalable Group Level Probabilistic Sparse Factor Analysis
Dec 14, 2016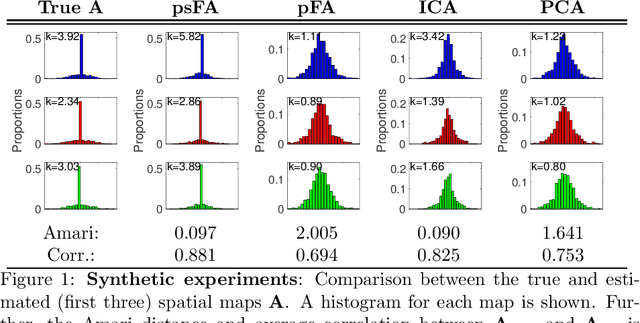

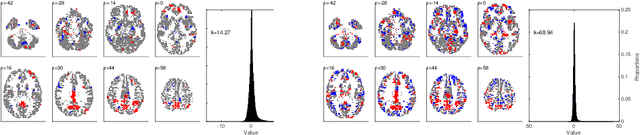
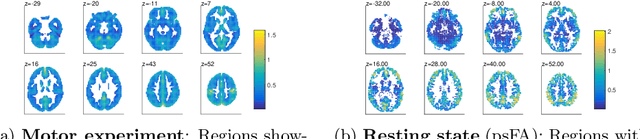
Abstract:Many data-driven approaches exist to extract neural representations of functional magnetic resonance imaging (fMRI) data, but most of them lack a proper probabilistic formulation. We propose a group level scalable probabilistic sparse factor analysis (psFA) allowing spatially sparse maps, component pruning using automatic relevance determination (ARD) and subject specific heteroscedastic spatial noise modeling. For task-based and resting state fMRI, we show that the sparsity constraint gives rise to components similar to those obtained by group independent component analysis. The noise modeling shows that noise is reduced in areas typically associated with activation by the experimental design. The psFA model identifies sparse components and the probabilistic setting provides a natural way to handle parameter uncertainties. The variational Bayesian framework easily extends to more complex noise models than the presently considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge