Grounded Computation & Consciousness: A Framework for Exploring Consciousness in Machines & Other Organisms

Computational modeling is a critical tool for understanding consciousness, but is it enough on its own? This paper discusses the necessity for an ontological basis of consciousness, and introduces a formal framework for grounding computational descriptions into an ontological substrate. Utilizing this technique, a method is demonstrated for estimating the difference in qualitative experience between two systems. This framework has wide applicability to computational theories of consciousness.

Reframing the Mind-Body Picture: Applying Formal Systems to the Relationship of Mind and Matter

This paper aims to show that a simple framework, utilizing basic formalisms from set theory and category theory, can clarify and inform our theories of the relation between mind and matter.

MAJORITY-3SAT (and Related Problems) in Polynomial Time

Majority-SAT is the problem of determining whether an input $n$-variable formula in conjunctive normal form (CNF) has at least $2^{n-1}$ satisfying assignments. Majority-SAT and related problems have been studied extensively in various AI communities interested in the complexity of probabilistic planning and inference. Although Majority-SAT has been known to be PP-complete for over 40 years, the complexity of a natural variant has remained open: Majority-$k$SAT, where the input CNF formula is restricted to have clause width at most $k$. We prove that for every $k$, Majority-$k$SAT is in P. In fact, for any positive integer $k$ and rational $\rho \in (0,1)$ with bounded denominator, we give an algorithm that can determine whether a given $k$-CNF has at least $\rho \cdot 2^n$ satisfying assignments, in deterministic linear time (whereas the previous best-known algorithm ran in exponential time). Our algorithms have interesting positive implications for counting complexity and the complexity of inference, significantly reducing the known complexities of related problems such as E-MAJ-$k$SAT and MAJ-MAJ-$k$SAT. At the heart of our approach is an efficient method for solving threshold counting problems by extracting sunflowers found in the corresponding set system of a $k$-CNF. We also show that the tractability of Majority-$k$SAT is somewhat fragile. For the closely related GtMajority-SAT problem (where we ask whether a given formula has greater than $2^{n-1}$ satisfying assignments) which is known to be PP-complete, we show that GtMajority-$k$SAT is in P for $k\le 3$, but becomes NP-complete for $k\geq 4$. These results are counterintuitive, because the ``natural'' classifications of these problems would have been PP-completeness, and because there is a stark difference in the complexity of GtMajority-$k$SAT and Majority-$k$SAT for all $k\ge 4$.

Context-Aware System Synthesis, Task Assignment, and Routing

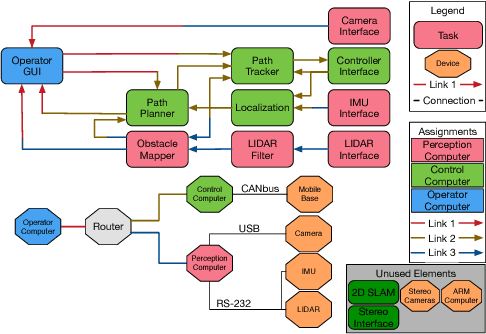
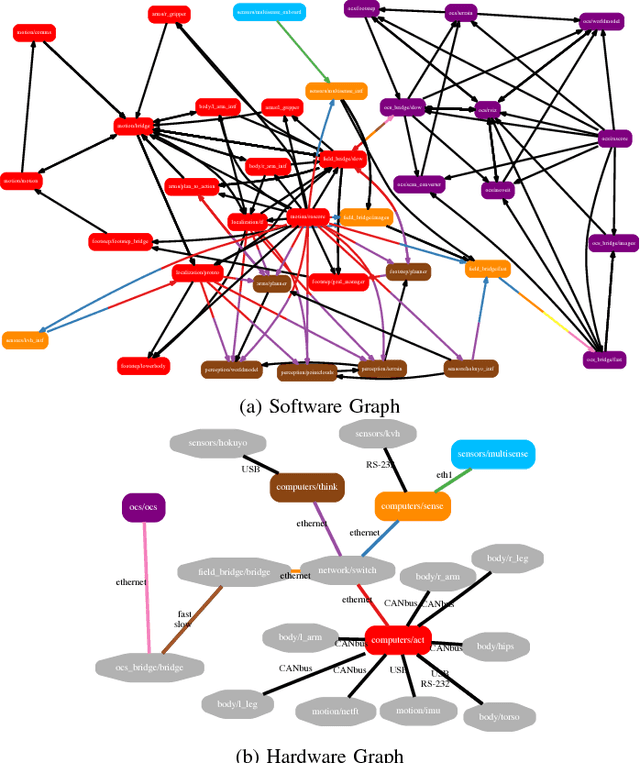
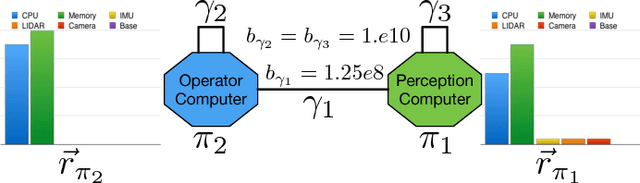
The design and organization of complex robotic systems traditionally requires laborious trial-and-error processes to ensure both hardware and software components are correctly connected with the resources necessary for computation. This paper presents a novel generalization of the quadratic assignment and routing problem, introducing formalisms for selecting components and interconnections to synthesize a complete system capable of providing some user-defined functionality. By introducing mission context, functional requirements, and modularity directly into the assignment problem, we derive a solution where components are automatically selected and then organized into an optimal hardware and software interconnection structure, all while respecting restrictions on component viability and required functionality. The ability to generate \emph{complete} functional systems directly from individual components reduces manual design effort by allowing for a guided exploration of the design space. Additionally, our formulation increases resiliency by quantifying resource margins and enabling adaptation of system structure in response to changing environments, hardware or software failure. The proposed formulation is cast as an integer linear program which is provably $\mathcal{NP}$-hard. Two case studies are developed and analyzed to highlight the expressiveness and complexity of problems that can be addressed by this approach: the first explores the iterative development of a ground-based search-and-rescue robot in a variety of mission contexts, while the second explores the large-scale, complex design of a humanoid disaster robot for the DARPA Robotics Challenge. Numerical simulations quantify real world performance and demonstrate tractable time complexity for the scale of problems encountered in many modern robotic systems.

Super-Linear Gate and Super-Quadratic Wire Lower Bounds for Depth-Two and Depth-Three Threshold Circuits

In order to formally understand the power of neural computing, we first need to crack the frontier of threshold circuits with two and three layers, a regime that has been surprisingly intractable to analyze. We prove the first super-linear gate lower bounds and the first super-quadratic wire lower bounds for depth-two linear threshold circuits with arbitrary weights, and depth-three majority circuits computing an explicit function. $\bullet$ We prove that for all $\epsilon\gg \sqrt{\log(n)/n}$, the linear-time computable Andreev's function cannot be computed on a $(1/2+\epsilon)$-fraction of $n$-bit inputs by depth-two linear threshold circuits of $o(\epsilon^3 n^{3/2}/\log^3 n)$ gates, nor can it be computed with $o(\epsilon^{3} n^{5/2}/\log^{7/2} n)$ wires. This establishes an average-case ``size hierarchy'' for threshold circuits, as Andreev's function is computable by uniform depth-two circuits of $o(n^3)$ linear threshold gates, and by uniform depth-three circuits of $O(n)$ majority gates. $\bullet$ We present a new function in $P$ based on small-biased sets, which we prove cannot be computed by a majority vote of depth-two linear threshold circuits with $o(n^{3/2}/\log^3 n)$ gates, nor with $o(n^{5/2}/\log^{7/2}n)$ wires. $\bullet$ We give tight average-case (gate and wire) complexity results for computing PARITY with depth-two threshold circuits; the answer turns out to be the same as for depth-two majority circuits. The key is a new random restriction lemma for linear threshold functions. Our main analytical tool is the Littlewood-Offord Lemma from additive combinatorics.

An Atypical Survey of Typical-Case Heuristic Algorithms

Heuristic approaches often do so well that they seem to pretty much always give the right answer. How close can heuristic algorithms get to always giving the right answer, without inducing seismic complexity-theoretic consequences? This article first discusses how a series of results by Berman, Buhrman, Hartmanis, Homer, Longpr\'{e}, Ogiwara, Sch\"{o}ening, and Watanabe, from the early 1970s through the early 1990s, explicitly or implicitly limited how well heuristic algorithms can do on NP-hard problems. In particular, many desirable levels of heuristic success cannot be obtained unless severe, highly unlikely complexity class collapses occur. Second, we survey work initiated by Goldreich and Wigderson, who showed how under plausible assumptions deterministic heuristics for randomized computation can achieve a very high frequency of correctness. Finally, we consider formal ways in which theory can help explain the effectiveness of heuristics that solve NP-hard problems in practice.

Alternation-Trading Proofs, Linear Programming, and Lower Bounds

A fertile area of recent research has demonstrated concrete polynomial time lower bounds for solving natural hard problems on restricted computational models. Among these problems are Satisfiability, Vertex Cover, Hamilton Path, Mod6-SAT, Majority-of-Majority-SAT, and Tautologies, to name a few. The proofs of these lower bounds follow a certain proof-by-contradiction strategy that we call alternation-trading. An important open problem is to determine how powerful such proofs can possibly be. We propose a methodology for studying these proofs that makes them amenable to both formal analysis and automated theorem proving. We prove that the search for better lower bounds can often be turned into a problem of solving a large series of linear programming instances. Implementing a small-scale theorem prover based on this result, we extract new human-readable time lower bounds for several problems. This framework can also be used to prove concrete limitations on the current techniques.