Context-Aware System Synthesis, Task Assignment, and Routing
Paper and Code
Aug 25, 2017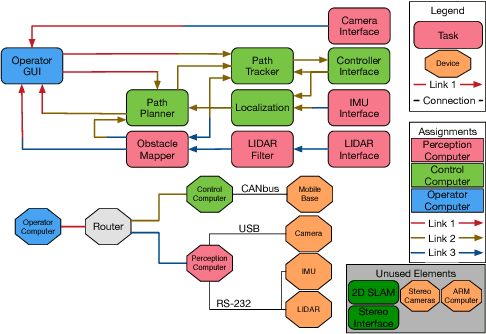
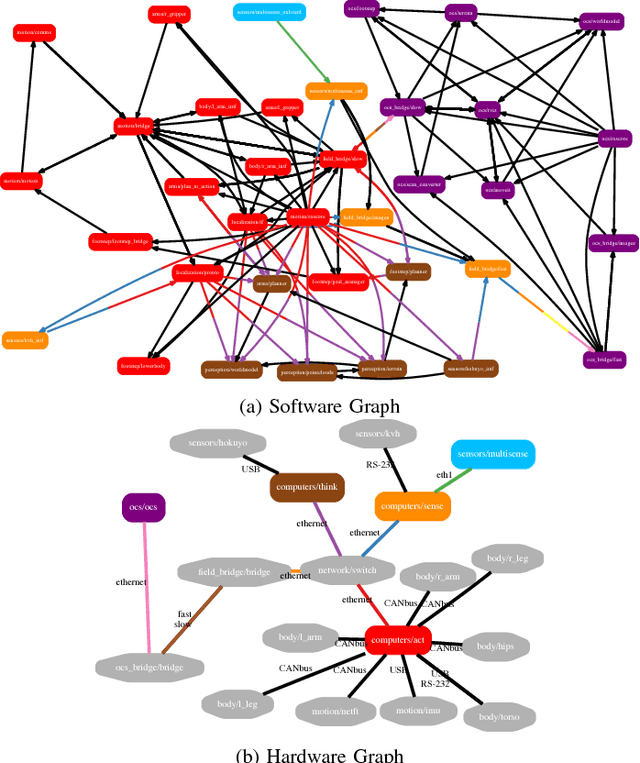
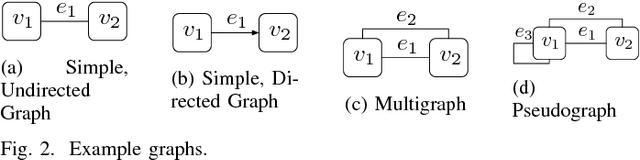
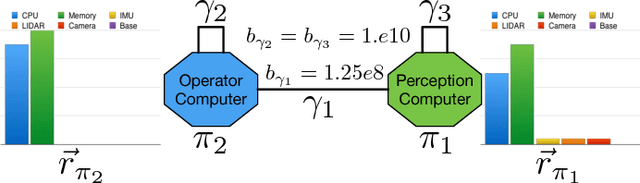
The design and organization of complex robotic systems traditionally requires laborious trial-and-error processes to ensure both hardware and software components are correctly connected with the resources necessary for computation. This paper presents a novel generalization of the quadratic assignment and routing problem, introducing formalisms for selecting components and interconnections to synthesize a complete system capable of providing some user-defined functionality. By introducing mission context, functional requirements, and modularity directly into the assignment problem, we derive a solution where components are automatically selected and then organized into an optimal hardware and software interconnection structure, all while respecting restrictions on component viability and required functionality. The ability to generate \emph{complete} functional systems directly from individual components reduces manual design effort by allowing for a guided exploration of the design space. Additionally, our formulation increases resiliency by quantifying resource margins and enabling adaptation of system structure in response to changing environments, hardware or software failure. The proposed formulation is cast as an integer linear program which is provably $\mathcal{NP}$-hard. Two case studies are developed and analyzed to highlight the expressiveness and complexity of problems that can be addressed by this approach: the first explores the iterative development of a ground-based search-and-rescue robot in a variety of mission contexts, while the second explores the large-scale, complex design of a humanoid disaster robot for the DARPA Robotics Challenge. Numerical simulations quantify real world performance and demonstrate tractable time complexity for the scale of problems encountered in many modern robotic systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge