Ryan Gardner
Adaptive Stress Testing: Finding Failure Events with Reinforcement Learning
Nov 06, 2018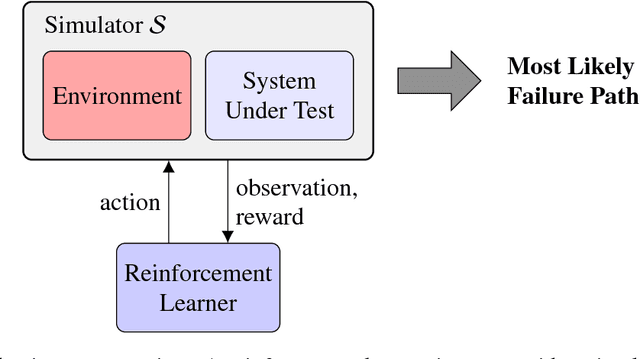
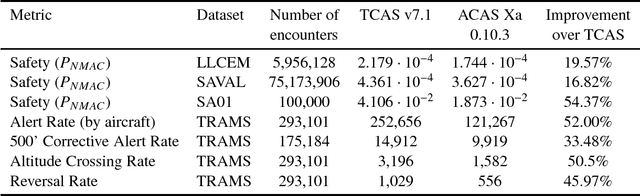
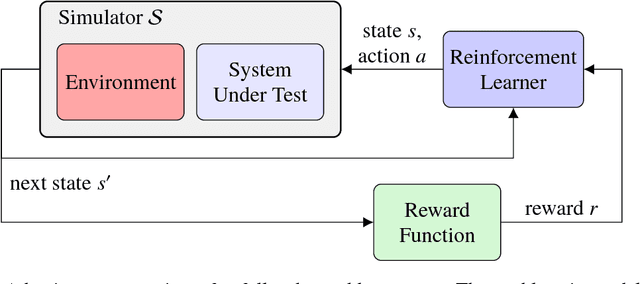
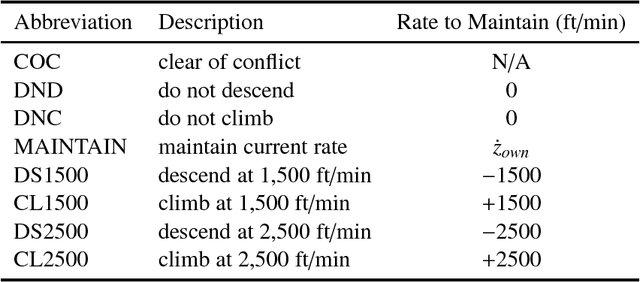
Abstract:Finding the most likely path to a set of failure states is important to the analysis of safety-critical dynamic systems. While efficient solutions exist for certain classes of systems, a scalable general solution for stochastic, partially-observable, and continuous-valued systems remains challenging. Existing approaches in formal and simulation-based methods either cannot scale to large systems or are computationally inefficient. This paper presents adaptive stress testing (AST), a framework for searching a simulator for the most likely path to a failure event. We formulate the problem as a Markov decision process and use reinforcement learning to optimize it. The approach is simulation-based and does not require internal knowledge of the system. As a result, the approach is very suitable for black box testing of large systems. We present formulations for both systems where the state is fully-observable and partially-observable. In the latter case, we present a modified Monte Carlo tree search algorithm that only requires access to the pseudorandom number generator of the simulator to overcome partial observability. We also present an extension of the framework, called differential adaptive stress testing (DAST), that can be used to find failures that occur in one system but not in another. This type of differential analysis is useful in applications such as regression testing, where one is concerned with finding areas of relative weakness compared to a baseline. We demonstrate the effectiveness of the approach on an aircraft collision avoidance application, where we stress test a prototype aircraft collision avoidance system to find high-probability scenarios of near mid-air collisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge