Pareto-Optimal Learning-Augmented Algorithms for Online k-Search Problems

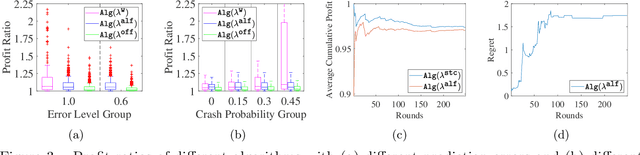
This paper leverages machine learned predictions to design online algorithms for the k-max and k-min search problems. Our algorithms can achieve performances competitive with the offline algorithm in hindsight when the predictions are accurate (i.e., consistency) and also provide worst-case guarantees when the predictions are arbitrarily wrong (i.e., robustness). Further, we show that our algorithms have attained the Pareto-optimal trade-off between consistency and robustness, where no other algorithms for k-max or k-min search can improve on the consistency for a given robustness. To demonstrate the performance of our algorithms, we evaluate them in experiments of buying and selling Bitcoin.

Pareto-Optimal Learning-Augmented Algorithms for Online Conversion Problems

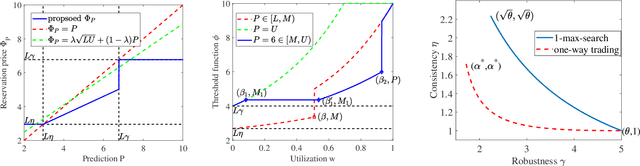
This paper leverages machine-learned predictions to design competitive algorithms for online conversion problems with the goal of improving the competitive ratio when predictions are accurate (i.e., consistency), while also guaranteeing a worst-case competitive ratio regardless of the prediction quality (i.e., robustness). We unify the algorithmic design of both integral and fractional conversion problems, which are also known as the 1-max-search and one-way trading problems, into a class of online threshold-based algorithms (OTA). By incorporating predictions into design of OTA, we achieve the Pareto-optimal trade-off of consistency and robustness, i.e., no online algorithm can achieve a better consistency guarantee given for a robustness guarantee. We demonstrate the performance of OTA using numerical experiments on Bitcoin conversion.